روشهای نمونهگیری در پژوهشهای علوم پزشکی (3)
تألیف:
دکتر احمد مردانی
مرکز تحقیقات سازمان انتقال خون، مؤسسه عالی آموزشی و پژوهشی طب انتقال خون
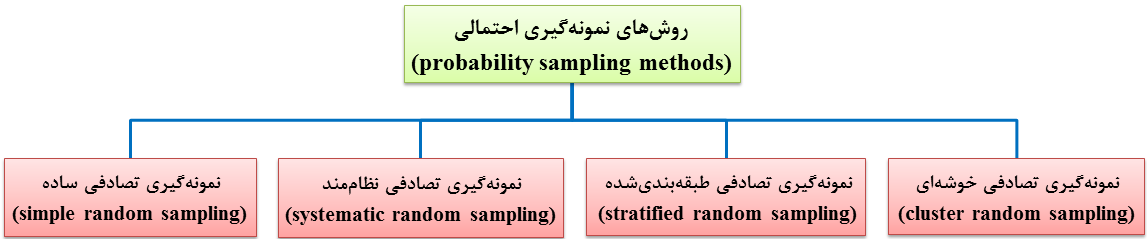
در نمونه گیری احتمالی و یا تصادفی (random sampling)، احتمال و یا شانس انتخاب هر عضوی از جمعیت مورد مطالعه معین و بزرگتر از صفر است و نمونه به روش تصادفی انتخاب میشود. به عبارت دیگر، هر عضوی از جمعیت مورد مطالعه، شانس و یا احتمال انتخاب برابر (EPS) دارد و این احتمال قابل اندازهگیری و تعیین است؛ بنابراین، نتایج آن قابل تعمیم به جمعیت هدف است و فاقد سوگرایی نمونه گیری و سوگرایی نظاممند (systematic bias) است. علاوه بر این، خطای نمونه گیری مشخص و قابل محاسبه و اندازهگیری است. بهترین راه دستیابی به نمونه واقعی و قابل اعتماد، بهکارگیری روش نمونهگیری احتمالی است که هر عضوی از جمعیت مورد مطالعه، شانس انتخاب مساوی و مشخصی دارد. لازم به ذکر است که سوگرایی نظاممند زمانی حادث میشود که بین نتایج حاصل از بررسی نمونه و بررسی جمعیت مورد مطالعه و یا جمعیت هدف، اختلاف وجود داشته باشد. انواع روشهای نمونه گیری احتمالیعبارتند از:
1- نمونه گیری تصادفی ساده (SRS)
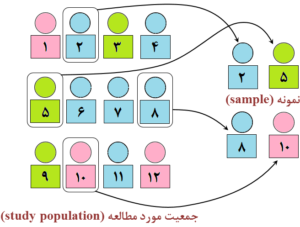
در نمونهگیری به روش تصادفی ساده، شانس و یا احتمال انتخاب همه اعضای جمعیت مورد مطالعه برابر و مشخص است و قوانین احتمال تعیین میکنند کدام نمونه انتخاب خواهد شد (شکل 7-1). انتخاب نمونه یا از طریق قرعهکشی (lottery method) و یا با استفاده از اعداد تصادفی (random numbers) انجام میشود.
شکل 7-1: نمای طرحواره یا شماتیک (schematic diagram) از نمونهگیری تصادفی ساده
(simple random sampling)
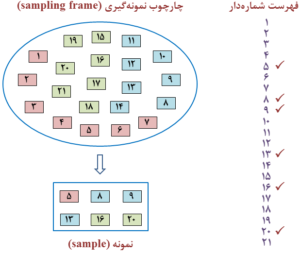
در روش قرعهکشی و استفاده از اعداد تصادفی، ابتدا کلیه اعضا و یا افراد جمعیت مورد مطالعه بهصورت تصادفی (randomly) شمارهبندی (numbering) میشوند. بهعبارت دیگر، بایستی فهرست یا لیست شمارهدار و یا چارچوب نمونهگیری تهیه شود (شکل 8-1).
شکل 8-1: نمای طرحواره یا شماتیک (schematic diagram) از تهیه فهرست شمارهدار و یا چارچوب نمونهگیری (sampling frame)
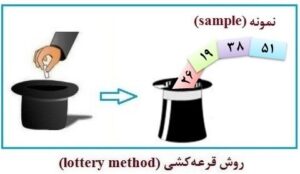
در روش قرعهکشی، به قید قرعه از بین شمارهها تعداد نمونه موردنیاز انتخاب میگردد (شکل 9-1). فرض کنید از بین 623 دانشآموز دختر یک مدرسهای میخواهیم نمونه 40 نفری برای محاسبه میزان هماتوکریت (hematocrit) و هموگلوبین (hemoglobin) خون انتخاب نماییم. برای این منظور مراحل زیر را انجام میدهیم:
الف- به هر یک از دانشآموزان عددی از 001 تا 623 تخصیص میدهیم (تهیه فهرست شمارهدار).
ب- این شمارهها را در یک ظرف (container) گذاشته و به تعداد 40 شماره به قید قرعه انتخاب میکنیم (قرعهکشی).
شکل 9-1: نمای طرحواره یا شماتیک (schematic diagram) از انتخاب نمونه به روش قرعهکشی
(lottery method)
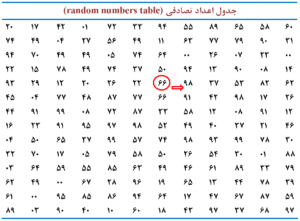
در روش اعداد تصادفی میتوان از جدول اعداد تصادفی و یا برنامههای رایانهای مانند برنامه صفحه گسترده یا اکسل (Excel) استفاده کرد. در روش استفاده از جدول اعداد تصادفی با توجه به ارقام حجم نمونه، اعداد را انتخاب میکنیم. به عنوان مثال، اگر حجم نمونه دو رقمی است، ابتدا یک عدد دو رقمی را بهصورت تصادفی، مثلاً با قرار دادن نوک مداد بر روی جدول اعداد تصادفی به عنوان نقطه یا شماره آغازین (starting point/number) انتخاب کرده و در ادامه با حرکت در جهتی که از قبل تعیین کردهایم (sampling direction)، مثلاً از چپ به راست، اعداد دو رقمی را تا تعداد نمونه موردنیاز انتخاب مینماییم (شکل 10-1). لازم به ذکر است که اگر عدد انتخابی تکراری باشد، نادیده گرفته شده و عدد بعدی انتخاب میشود.
به طورکلی، نمونهگیری به روش تصادفی ساده به دو شکل قابل انجام است که عبارتند از:
1- نمونهگیری تصادفی ساده بدون جایگزینی (SRSWOR)
در این روش، هر عضو نمونهگیری فقط یکبار شانس انتخاب شدن به عنوان نمونه را دارد. این روش رایجتر است و در عمل تمامی نمونهگیریها به روش تصادفی ساده، بدون جایگزینی انجام میشود.
2- نمونهگیری تصادفی ساده با جایگزینی (SRSWR)
در این روش نمونهگیری تصادفی ساده، هر عضو نمونهگیری بیش از یکبار شانس انتخاب شدن به عنوان نمونه را دارد. به عنوان مثال، اگر ما از استخری یک ماهی صید کنیم و پس از ثبت ویژگیهای موردنظر، آن را به استخر بازگردانیم، به این روش نمونهگیری تصادفی ساده با جایگزینی گویند. درصورتیکه ماهی را به استخر برنگردانیم، روش نمونهگیری تصادفی ساده بدون جایگزینی است.
شکل 10-1: نمای طرحواره یا شماتیک (schematic diagram) از انتخاب نمونه با استفاده از جدول اعداد تصادفی (random numbers table)
در شکل، نقطه آغازین (starting point) و جهت حرکت مشخص شده است.
آسانی قابلیت اندازهگیری خطای نمونهگیری، سادگی (simplicity) انجام و نبود سوگرایی انتخاب نمونه یا نمونهگیری به دلیل شانس مساوی انتخاب، از مزایای روش نمونهگیری تصادفی ساده است. معایب این روش عبارتند از:
1- احتیاج به چارچوب نمونهگیری دارد (تهیه فهرست شمارهدار)، البته اگر چارچوب نمونهگیری بزرگ باشد، نمونهگیری تصادفی ساده قابلیت اجرایی نخواهد داشت.
2- ممکن است نمونه انتخابشده، بهترین معرف و یا نماینده جمعیت مورد مطالعه نباشد.
3- هزینهبر و زمانبر است، به ویژه هنگامی که پراکندگی جمعیت هدف و حجم نمونه زیاد باشد.
4- ممکن است به دلیل پراکندگی نمونههای انتخابشده، دسترسی به آنها سخت باشد.
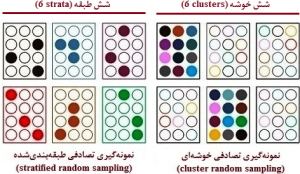
نکته 1: ممکن است به دلیل تصادفی بودن انتخاب، نمونه انتخابشده منعکسکننده ترکیب جمعیتی از نظر جنس، سن، شغل و سایر متغیرهای زمینهای در روش نمونهگیری تصادفی ساده نباشد، به همین دلیل، رخداد خطای نمونهگیری در این روش امکانپذیر است. این نقص در روش نمونهگیری تصادفی طبقهبندیشده (stratified random sampling) با طبقهبندی جمعیت به زیرگروهها برطرف میشود.
نکته 2: نمونهگیری تصادفی ساده، زمانی قابل اجرا است که جمعیت مورد مطالعه کوچک، همگن (homogeneous) و به آسانی در دسترس باشد.
نکته 3: واژه تصادفی به معنای شانس انتخاب مساوی هر عضو جمعیت مورد مطالعه است، بهطوریکه انتخاب هر عضوی مستقل از دیگر اعضا بوده و هیچ تأثیری بر انتخاب عضو دیگر ندارد. از دیگر ویژگیهای انتخاب تصادفی این است که سوگرایی محقق (investigator bias) در انتخاب نمونه وارد نیست.
نکته 4: واژه simple به معنای آسان (easy) و یا غیرپیچیده (uncomplicated) نیست. روش نمونهگیری تصادفی ساده میتواند کاملاً پیچیده و زمانبر باشد، به ویژه اگر حجم نمونه زیاد باشد.
نکته 5: نمونهگیری تصادفی ساده حداقل در یک مرحله از سه نوع دیگر روشهای نمونه گیری احتمالی یعنی نمونهگیری تصادفی نظاممند یا سیستماتیک (systematic)، طبقهبندیشده و خوشهای (cluster) مورد استفاده قرار میگیرد.
نکته 6: جدول اعداد تصادفی، رایجترین و دقیقترین روش استفادهشده در نمونهگیری تصادفی ساده است.
نکته 7: در روش اعداد تصادفی، اگر حجم نمونه کم باشد از جدول اعداد تصادفی استفاده میشود، اما اگر حجم نمونه زیاد است، ترجیحاً استفاده از برنامههای رایانهای مانند برنامه صفحه گسترده یا اکسل (Excel) توصیه میگردد.
2- نمونهگیری تصادفی نظاممند یا سیستماتیک (systematic random sampling)
در این روش، حجم نمونه یا تعداد نمونه موردنیاز (n) از جمعیت مورد مطالعه (N) انتخاب میگردد. برای این منظور، ابتدا چارچوب نمونهگیری (فهرست شمارهدار) از جمعیت مورد مطالعه تهیه مینماییم و در ادامه پس از تعیین حجم نمونه (n)، فاصله نمونهگیری (sampling interval) یا اندازه فاصله (interval size) را که با k نمایش میدهند، بهصورت زیر محاسبه میکنیم.
k=N/n
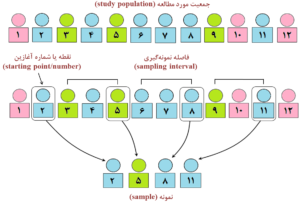
در ادامه، از شماره یک تا k، یک شماره (عدد) بهطور تصادفی انتخاب میکنیم (انتخاب اولین نمونه) و نمونههای بعدی را با فاصله k از عدد مذکور و یا اولین نمونه انتخاب مینماییم (شکل 11-1). به عنوان مثال، اگر بخواهیم از بین ۱۰۰۰ بیمار (جمعیت مورد مطالعه) ۱۰۰ نفر (نمونه موردنیاز) را با استفاده از این روش نمونهگیری کنیم، ابتدا فهرست شمارهدار مثلاً به ترتیب حروف الفبا (alphabetical order) از هزار نفر تهیه میکنیم و در ادامه، فاصله نمونهگیری را محاسبه مینماییم که 10 میشود. در مرحله بعد یک نفر از شماره یک تا ۱۰ را بهطور تصادفی انتخاب میکنیم. اگر عدد تصادفی انتخابشده شماره پنج باشد، نمونههای بعدی با فاصله دهتایی یعنی شمارههای ۱۵، ۲۵، ۳۵، ۴۵، ۵۵ و … تا حصول 100 نمونه انتخاب میشوند.
در نمونهگیری به روش نظاممند همانند روش نمونهگیری تصادفی ساده، شانس و یا احتمال انتخاب همه اعضای جمعیت مورد مطالعه برابر است و برخلاف روش تصادفی ساده، فقط اولین نمونه بهصورت تصادفی انتخاب میشود.
هزینه و زمان کمتر در مقایسه با روش نمونهگیری تصادفی ساده و سادگی انجام از مهمترین مزایای روش نمونهگیری تصادفی سیستماتیک است.
معایب این روش عبارتند از:
1- احتیاج به چارچوب نمونهگیری دارد (تهیه فهرست شمارهدار).
2- ممکن است نمونه انتخابشده، بهترین معرف و یا نماینده جمعیت مورد مطالعه نباشد.
3- اگر فاصله نمونهگیری بر تغییرهای منظم در جمعیت مورد مطالعه منطبق شود، سوگرایی رخ میدهد.
نکته 1: تا زمانی که نقطه یا شماره آغازین نمونهگیری یا اولین نمونه بهصورت تصادفی انتخاب میشود، روش نمونهگیری تصادفی نظاممند جزو روشهای نمونهگیری احتمالی است.
نکته 2: اگر حاصل تقسیم جمعیت مورد مطالعه (N) بر حجم نمونه یا تعداد نمونه موردنیاز (n)، عدد کسری بود، به نزدیکترین عدد صحیح گرد (round) کنید.
شکل 11-1: نمای طرحواره یا شماتیک (schematic diagram) از نمونهگیری تصادفی نظاممند (systematic random sampling)
در شکل، نقطه یا شماره آغازین (starting point/number) و فاصله نمونهگیری (sampling interval) مشخص شده است
3-نمونه گیری تصادفی طبقهبندیشده
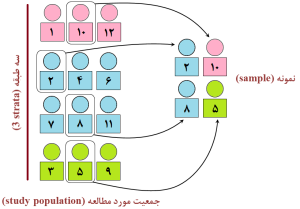
در این روش نمونهگیری، جمعیت مورد مطالعه بر اساس یک ویژگی و یا ملاک (criterion) متمایزکننده مانند شغل، سطح سواد، وضعیت اقتصادی، میزان درآمد، جنس و یا سن به طبقههای مجزا (separate strata) و بدون همپوشانی یا non-overlapping (یعنی تعلق هر فرد فقط و فقط به یکی از طبقهها) تقسیم میشود. در ادامه از هر طبقه (stratum) به تعداد مورد نیاز و متناسب (proportionate) با حجم طبقه و یا به تعداد مساوی و نامتناسب (disproportionate) با حجم طبقه، نمونه بهصورت تصادفی ساده (در اغلب موارد) و یا تصادفی نظاممند انتخاب میگردد (شکل 12-1).
به عنوان مثال، از یک جمعیت مورد مطالعه ۱۰۰۰ نفری که ۱۵ درصد آن دانشجو، ۲۰ درصد کارمند اداری، ۳۰ درصد کارگر و ۳۵ درصد کشاورز هستند، میخواهیم ۴۰۰ نفر (نمونه) انتخاب کنیم. در مرحله اول، تعداد نمونه مورد نیاز از هر طبقه را متناسب با حجم طبقه (درصدهای فوق) معین میکنیم که به شرح زیر است.
– تعداد افراد (نمونه) از بین دانشجویان: 60 =0/15 × ۴۰۰
– تعداد افراد (نمونه) از بین کارمندان اداری: ۸۰ =0/20 × ۴۰۰
– تعداد افراد (نمونه) از بین کارگران: ۱۲۰ =0/30 × ۴۰۰
– تعداد افراد (نمونه) از بین کشاورزان: 140 =0/35 × ۴۰۰
مجموع افراد انتخابشده از طبقهها، ۴۰۰ نفر خواهد بود (۴۰۰ =۱۴۰+۱۲۰+۸۰+۶۰).
در مرحله دوم، از هر یک از طبقهها، تعداد نمونه مورد نظر را با استفاده از روش تصادفی ساده و یا سیستماتیک انتخاب مینماییم. در این مثال اگر بخواهیم از هر طبقه به تعداد مساوی و نامتناسب با حجم طبقه، نمونه انتخاب کنیم، بایستی حجم نمونه (400) را بر تعداد طبقه (چهار) تقسیم نماییم (400/4) و به تعداد حاصله (100)، از هر طبقه نمونهگیری کنیم.
شکل 12-1: نمای طرحواره یا شماتیک (schematic diagram)
از نمونه گیری تصادفی طبقهبندیشده
(stratified random sampling)
مزیت بزرگ این روش نمونهگیری بر روشهای نمونه گیری تصادفی ساده و نظاممند این است که توزیع جمعیتهای مختلف در نمونه با جمعیت مورد مطالعه مطابقت دارد و نمونه انتخابشده، بهترین معرف و یا نماینده جمعیت مورد مطالعه است. امکان تجزیه و تحلیل جداگانه برای هر یک از طبقهها، آسانی انجام و کارایی آماری بالاتر، از دیگر مزایای نمونه گیری طبقهبندیشده است. از معایب این روش نمونهگیری میتوان به خطای تقسیمبندی (classification error)، زمانبری، هزینهبری، تهیه چارچوب نمونه گیری جداگانه برای هر طبقه و سختی محاسبه خطای نمونهگیری اشاره کرد. لازم به ذکر است که احتمال و یا شانس انتخاب برای تمامی اعضای جمعیت مورد مطالعه در روش نمونهگیری تصادفی طبقهبندیشده همانند دیگر روشهای نمونهگیری احتمالی، یکسان است.
نکته 1: در جمعیتهای ناهمگن و یا نامتجانس که توزیع جمعیت در گروهها و طبقههای مختلف متفاوت است، از روش نمونه گیری تصادفی طبقهبندیشده استفاده میشود. البته زمانی میتوان از روش نمونه گیری تصادفی طبقهبندیشده استفاده کرد که نسبت هر طبقه در جمعیت مورد مطالعه نیز مشخص باشد.
نکته 2: در روش نمونه گیری تصادفی طبقهبندیشده بایستی ویژگی متمایزکننده و یا استفادهشده برای طبقهبندی با هدف اصلی مطالعه، ارتباط منطقیتری داشته باشد؛ برای مثال در مطالعهای با عنوان “اندازهگیری قطر تراشه از روی کلیشه رادیوگرافی”، از آنجایی که اندازه تراشه بر حسب سن بیمار تغییر میکند؛ میتوان برحسب سن، بیماران را طبقهبندی کرد. البته علاوه بر سن میتوان بیماران را برحسب جنس، مرحله بیماری و دوره بیماری نیز تقسیمبندی نمود. آنچه در طبقهبندی از اهمیت بالایی برخوردار است، انتخاب خصوصیتی است که ارتباط قوی و منطقی با هدف کلی تحقیق و پژوهش دارد.
نکته 3: هر چقدر شباهت اعضای داخل یک طبقه به هم بیشتر باشد (homogeneity)، نتایج بهتر و دقیقتری به دلیل کاهش واریانس (variance) حاصل خواهد شد.
نکته 4: نمونه گیری تصادفی طبقهبندیشده و نمونهگیری سهمیهای کاملاً شبیه هم هستند؛ بهجز انتخاب نمونه که در نمونه گیری تصادفی طبقهبندیشده به صورت تصادفی و در نمونهگیری سهمیهای به صورت غیرتصادفی است. به همین دلیل، گاهی به نمونهگیری تصادفی طبقهبندیشده، نمونـه گیری تصادفی سهمیهای (quota random sampling) نیز اطلاق میشود.
نکته 5: اگر ویژگی متمایزکننده جزو عوامل مسبب تغییر معنادار باشد، نمونهگیری تصادفی طبقهبندیشده روشی مؤثر برای کاهش واریانس است.
نکته 6: انتخاب نمونه از هر طبقه در نمونهگیری به روش تصادفی طبقهبندیشده به دو روش متناسب با حجم طبقه (proportionate) و نامتناسب با حجم طبقه (disproportionate) قابل انجام است. بر همین اساس، نمونهگیری به روش تصادفی طبقهبندیشده را به دو نوع تقسیمبندی مینمایند که عبارتند از:
الف- نمونهگیری تصادفی طبقهبندیشده متناسب (PSRS)
ب- نمونهگیری تصادفی طبقهبندیشده نامتناسب (DSRS)
لازم به ذکر است که روش نامتناسب، سادهتر و روش متناسب، دقیقتر و واقعیتر است.
4- نمونه گیری احتمالی خوشهای (cluster random sampling)
در نمونهگیری تصادفی خوشهای، ابتدا بایستی محیط مورد پژوهش یا قلمرو مکانی را برحسب عوامل مؤثر در موضوع مورد بررسی تقسیمبندی کرد و یا از تقسیمبندیهای موجود مرتبط مانند مناطق جغرافیایی و نواحی شهری، آموزشی، پستی و … استفاده نمود. در ادامه، جمعیت مورد مطالعه را بر اساس موضوع مورد بررسی خوشهبندی قرار داد، سپس به صورت تصادفی (در اغلب موارد به روش تصادفی ساده و گاهی نظاممند) تعدادی خوشه (cluster) مانند خانوادهها، مدارس، بیمارستانها، مراکز درمانی، بلوکهای شهری، دهکدهها و … را از مناطق و یا نواحی تقسیمبندیشده انتخاب نمود.
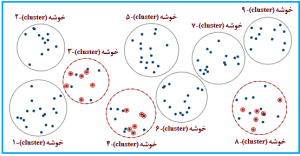
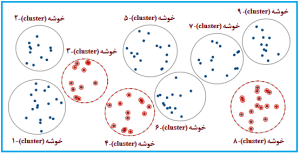
در نمونه گیری تصادفی خوشهای، نمونه به صورت تصادفی (در اغلب موارد به روش تصادفی ساده و گاهی نظاممند و یا طبقهبندیشده) از گروهها یا خوشههای منتخب (نمونهگیری تصادفی خوشهای دو مرحلهای) و یا تمامی اعضای هر خوشه (نمونهگیری تصادفی خوشهای یک مرحلهای) به عنوان نمونه انتخاب میشود (شکلهای 13-1 و 14-1)، بنابراین، ابتدا باید فهرستی از خوشههای هر منطقه و یا ناحیه مورد پژوهش تهیه شود و در ادامه پس از انتخاب تصادفی خوشهها، به صورت تصادفی از خوشهها نمونه گیری گردد؛ برای مثال اگر بخواهیم بهداشت دهان و دندان دانشآموزان دبستانهای دخترانه شهر تهران را بررسی کنیم، ابتدا لیست تمام مدارس ابتدایی دخترانه شهر تهران را به تفکیک منطقه شهرداری تهیه مینماییم.
در ادامه، به صورت تصادفی از هر منطقه شهرداری یک و یا چند مدرسه (خوشه) را انتخاب و به صورت تصادفی از مدارس منتخب، دانشآموزان (نمونه) را انتخاب میکنیم (نمونهگیری). لازم به ذکر است که احتمال و یا شانس انتخاب برای تمامی اعضای جمعیت مورد مطالعه در روش نمونهگیری تصادفی خوشهای همانند دیگر روشهای نمونهگیری احتمالی، یکسان است.
شکل 13-1: نمای طرحواره یا شماتیک (schematic diagram)
از نمونهگیری تصادفی خوشهای دومرحلهای
(two-stage cluster random sampling)
شکل 14-1: نمای طرحواره یا شماتیک (schematic diagram)
از نمونه گیری تصادفی خوشهای یک مرحلهای
(one-stage cluster random sampling)
دقت نمونه گیری به روش تصادفی خوشهای به دلیل فزونی خطای نمونهگیری کمتر از روشهای تصادفی ساده، نظاممند یا سیستماتیک و طبقهبندیشده است، اما صرفهجویی در هزینهها و زمان و عدم نیاز به اسامی همه اعضای جمعیت مورد مطالعه از مزایای این روش نمونهگیری است. به عبارت دیگر، سریع و ارزان است.
نکته 1: محیط مورد پژوهش یا قلمرو مکانی عبارت است از مکانی که نمونههای مورد مطالعه از آنجا گرفته میشود.
نکته 2: اگر همه خوشههای یک منطقه و یا ناحیه مورد پژوهش، ویژگیهای نزدیک به هم و یا همگنی بیشتری داشته باشند؛ انتخاب یک خوشه از هر منطقه کافی خواهد بود. در غیر این حالت، بایستی تعداد خوشههای بیشتری را از هر منطقه انتخاب کرد. به عبارت دیگر، اندازه یا حجم نمونه را به 1/5تا 2/5 برابر افزایش میدهند.
نکته 3: وقتی حجم و پراکندگی جمعیت مورد مطالعه خیلی زیاد باشد، تهیه چارچوب نمونهگیری دقیق و درست تقریباً غیرممکن است و یا نیاز به هزینه بالا دارد و زمانبر است؛ بنابراین، نمونهگیری به روشهای تصادفی ساده و نظاممند در چنین مواردی غیرممکن است و نمونهگیری به روش تصادفی خوشهای راهکار مناسبی است.
نکته 4: اگر تمامی اعضای خوشههای منتخب نمونهگیری شوند؛ به این روش، نمونهگیری تصادفی خوشهای یک مرحلهای (one-stage cluster random sampling) گویند. در صورتی که از اعضای خوشههای منتخب، تعدادی به عنـــــــــــــــوان نمونه انتخاب شونـــــد، نمونـــــهگیری تصادفی خوشهای دو مرحلهای (two-stage cluster random sampling) نامیده میشود.
نکته 5: هر چقدر شباهت اعضای داخل یک خوشه به هم کمتر باشد (heterogeneity)، نتایج بهتر و دقیقتری حاصل خواهد شد.
نکته 6: ازآنجاییکه تقسیمبندی قلمرو مکانی یا محیط مورد پژوهش در نمونهگیری تصادفی خوشهای بهطور متداول بر اساس مناطق جغرافیایی و یا فواصل مکانی انجام میگیرد، استفاده از این روش نمونهگیری در پژوهشهای همهگیرشناسی یا اپیدمیولوژی بیشتر از بررسیهای بالینی رایج است. رایجترین روش تقسیمبندی و یا خوشهبندی در نمونهگیری تصادفی خوشهای، خوشهبندی جغرافیایی است.
نکته 7: تفاوت نمونهگیری تصادفی طبقهبندیشده و خوشهای این است که در نمونهگیری تصادفی طبقهبندیشده، نمونه از هر طبقهای متناسب و یا نامتناسب با حجم طبقه گرفته میشود، اما در نمونهگیری خوشهای فقط از خوشههای منتخب نمونهگیری انجام میگیرد (شکل 15-1). علاوه بر این، بهترین نتایج مطالعه زمانی حاصل میشوند که اعضای داخل طبقهها همگنی بیشتر و اعضای داخل خوشهها همگنی کمتری داشته باشند.
شکل 15-1: نمای طرحواره یا شماتیک (schematic diagram)
از تفاوت نمونهگیری تصادفی طبقهبندیشده
(stratified random sampling) و خوشهای (cluster random sampling)
نکته 8: از نمونه گیری احتمالی خوشــــهای اغلب برای ارزیابی پوشش ایمنیزایی یک واکسن (assessing vaccination coverage) در همهگیرشناسی یا اپیدمیولوژی استفاده میشود؛ همچنین، روش بسیار مفیدی برای پژوهشهای همهگیرشناسی میدانی (field epidemiological researches) و مدیران بهداشت است.
نکته 9: در نمونهگیری تصادفی خوشهای یک مرحلهای برخلاف دیگر روشهای نمونهگیری، خوشهها واحدهای نمونهگیری هستند.
نکته 10: از آنجایی که روش نمونه گیری خوشهای معمولاً زمانی که حجم جمعیت مورد مطالعه زیاد باشد، مورد استفاده قرار میگیرد، گاهی به نمونه گیری خوشهای، نمونهگیری ناحیهای و یا منطقهای (area sampling) نیز اطلاق میشود.
نکته 11: وقتی جمعیت مورد مطالعه غیرهمگن است، میتوان از روشهای نمونهگیری سهمیهای، طبقهبندیشده و یا خوشهای استفاده کرد.
5- نمونه گیری احتمالی چندمرحلهای (multistage random sampling)
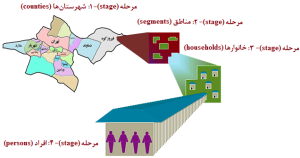
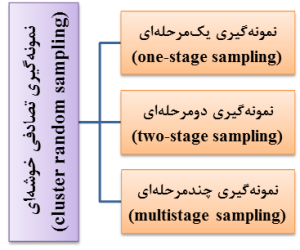
نمونه گیری تصادفی چندمرحلهای، شکل پیچیده نمونه گیری تصادفی خوشهای است (شکل 16-1). به عبارت دیگر، روش نمونهگیری تصادفی چندمرحلهای جزو روش نمونهگیری تصادفی خوشهای تقسیمبندی میشود (شکل 17-1)؛ به همین دلیل، در برخی منابع، روشهای نمونه گیری احتمالی و یا تصادفی را به چهار روش تصادفی ساده، نظاممند، طبقهبندیشده و خوشهای تقسیمبندی میکنند (شکل 18-1).
شکل 16-1: نمای طرحواره یا شماتیک (schematic diagram)
از نمونه گیری تصادفی چندمرحلهای
(multistage random sampling)
نکته: با افزایش مراحل نمونه گیری، احتمال رخداد خطای نمونهگیری بیشتر میشود. برای تقلیل این خطا بایستی حجم نمونه را افزایش داد.
این روش نمونه گیری، زمانی که حجم و پراکندگی جمعیت مورد مطالعه خیلی زیاد باشد، مثلاً پروژههای شهری، استانی و ملی، مورد استفاده قرار میگیرد؛ به عنوان مثال برای “بررسی مصرف سیگار در دانشآموزان مقطع تحصیلی متوسطه شهر تهران” بایستی مراحل زیر را طی کرد:
1- تقسیمبندی شهر تهران به چند منطقه آموزشی و یا استفاده از تقسیمبندی آموزشی موجود
2- تهیه فهرست از مدارس پسرانه و دخترانه هر منطقه به تفکیک مقاطع تحصیلی متوسطه اول و دوم (خوشهبندی)
3- انتخاب تصادفی سه مدرسه پسرانه و سه مدرسه دخترانه از هر مقطع تحصیلی در هر منطقه (انتخاب خوشه-1)
4- انتخاب تصادفی یک کلاس از هر مقطع و پایه تحصیلی در هر مدرسه منتخب (انتخاب خوشه-2)
5- انتخاب تصادفی نمونه از دانشآموزان هر کلاس (انتخاب نمونه)
شکل 17-1: تقسیمبندی روشهای نمونهگیری تصادفی خوشهای
(cluster random sampling)
شکل 18-1: تقسیمبندی روشهای نمونه گیری احتمالی
(probability sampling methods)
https://economictimes.indiatimes.com/definition/random-sampling
برای دانلود پی دی اف بر روی لینک زیر کلیک کنید
ورود / ثبت نام