همهی قوانین را نقض کنید – پاسخ به پرسشهای بخش نخست (n=1)
استن وستگارد، MS
آگوست 2015
توضیح مترجم:
این سلسله مقالات شامل 6 بخش است که بهصورت ماهانه بر روی وبسایت Westgard.com قرار میگیرد. ترجمه و انتشار این مطالب در ماهنامهی اخبار آزمایشگاهی و نیز استفاده از طرح وبسایت یادشده با مجوز شرکت Westgard QC انجام میشود؛ امری که مایهی تقدیر و تشکر فراوان از متصدیان آن شرکت بهویژه جناب آقای استن وستگارد است.
از آنجائی که ممکن است برخی مطالب مطرحشده در این مقالات نیازمند روشنگری بیشتری باشد، خوانندگان محترم میتوانند نکات، نظرات و پرسشهایشان را به رایانامهی labnews2003@gmail.com ارسال کنند تا در شمارههای بعدی به بحث گذاشته شود.
قدردرانی: بر خود لازم میدانم از جناب آقای دکتر محمدرضا عابدی سردبیر محترم این ماهنامه و همکاران تلاشگر ایشان به خاطر همکاری بیدریغ ایشان و از دوست و همکار گرامی جناب آقای دکتر مهدی صابونی به خاطر قبول زحمت ویرایش این مطالب صمیمانه تشکر نمایم.
حسن بیات؛ دانشآموختهی علوم آزمایشگاهی
پاسخها
مجموعه دادههای زیر دارای میانگین 47 و SD برابر 3 هستند. به شما نمیگویم که این دادهها مربوط به چه آزمایشی است یا اینکه چه واحدی به کار گرفته شده است زیرا اینها به این تمرین مربوط نمیشود. همچنین به خطای کل مجاز یا CV یا نامیزانی (عدم صحت) اشاره نمیکنم. همهی اینها پسازاین که اساس پایش کیفیت و رسم نمودار را دانستیم اهمیت پیدا میکند.
برای راحتی کار، دادهها را به نمرهی z[1] تبدیل کردهایم که نشان میدهد فاصلهی یک نقطه از میانگین چند SD و در چه جهتی است؛ برای مثال، اگر یک داده 42/5 باشــد آنگاه اختلاف آن با میانگین برابر 4/5- میشود (4/5- = 47 – 42/5) و از تقسیم این اختلاف به انحراف معیار معلوم میشود که این داده بهاندازهی 1/5 انحراف معیار زیر میانگین است (1/5- = 3 ÷ 4/5-)، بنابراین نمرهی z عدد 42/5 برابر 1/5 است.
| قانون نقض شده | نمرهی z | نتیجه | سنجش کنترل |
| -1.5 | 42.5 | 1 | |
| 2.7 | 55.1 | 2 | |
| -0.2 | 46.4 | 3 | |
| 0 | 47.0 | 4 | |
| -1.3 | 43.1 | 5 | |
| 1:3s rule | 3.3 | 56.9 | 6 |
| -1.9 | 41.3 | 7 | |
| -0.7 | 44.9 | 8 | |
| -0.5 | 45.5 | 9 | |
| -1.9 | 41.3 | 10 | |
| 0 | 47.0 | 11 | |
| 1:3s rule | -3.1 | 37.7 | 12 |
| -1.8 | 41.6 | 13 | |
| 2:2 rule | 2.1 | 53.3 | 14 |
| 2.8 | 55.4 | 15 | |
| -0.8 | 44.6 | 16 | |
| 0.1 | 47.3 | 17 | |
| 0.4 | 48.2 | 18 | |
| -1.9 | 41.3 | 19 | |
| -1.4 | 42.8 | 20 | |
| -0.9 | 44.3 | 21 | |
| 0.2 | 47.6 | 22 | |
| -0.9 | 44.3 | 23 | |
| -0.4 | 45.8 | 24 | |
| 0.2 | 47.6 | 25 | |
| 2:2s rule | -2.4 | 39.8 | 26 |
| -2.4 | 39.8 | 27 | |
| 1.3 | 50.9 | 28 | |
| 0.9 | 49.7 | 29 | |
| -0.5 | 45.5 | 30 | |
| -0.6 | 45.2 | 31 | |
| 0.1 | 47.3 | 32 | |
| 0.3 | 47.9 | 33 | |
| -0.9 | 44.3 | 34 | |
| -2.3 | 40.1 | 35 | |
| 0.4 | 48.2 | 36 | |
| 4:1s rule | -2.1 | 40.7 | 37 |
| -1.7 | 41.9 | 38 | |
| -1.2 | 43.4 | 39 | |
| -1.1 | 43.7 | 40 | |
| 0.9 | 49.7 | 41 | |
| -1.6 | 42.2 | 42 | |
| 1.7 | 52.1 | 43 | |
| 8:x rule | -0.8 | 44.6 | 44 |
| -0.6 | 45.2 | 45 | |
| -0.4 | 45.8 | 46 | |
| -1.8 | 41.6 | 47 | |
| -1.9 | 41.3 | 48 | |
| -0.7 | 44.9 | 49 | |
| -1.1 | 43.7 | 50 | |
| -0.6 | 45.2 | 51 | |
| 4:1s rule | 1.2 | 50.6 | 52 |
| 1.1 | 50.3 | 53 | |
| 1.4 | 51.2 | 54 | |
| 1.5 | 51.5 | 55 | |
| -0.9 | 44.3 | 56 | |
| -1.8 | 41.6 | 57 | |
| 10:x rule | 2.3 | 53.9 | 58 |
| 0.6 | 48.8 | 59 | |
| 0.4 | 48.2 | 60 | |
| 1.2 | 50.6 | 61 | |
| 0.4 | 48.2 | 62 | |
| 0.5 | 48.5 | 63 | |
| 0.9 | 49.7 | 64 | |
| 1.3 | 50.9 | 65 | |
| 0.1 | 47.3 | 66 | |
| 0.4 | 48.2 | 67 | |
| 8:x rule | -0.4 | 45.8 | 68 |
| -1.3 | 43.1 | 69 | |
| -1.1 | 43.7 | 70 | |
| -1.4 | 42.8 | 71 | |
| -0.7 | 44.9 | 72 | |
| -1.5 | 42.5 | 73 | |
| -0.3 | 46.1 | 74 | |
| -0.5 | 45.5 | 75 | |
| 0.3 | 47.9 | 76 | |
| 0.1 | 47.3 | 77 | |
| 1.2 | 50.6 | 78 | |
| -1.1 | 43.7 | 79 | |
| 0 | 47.0 | 80 | |
| 1.3 | 50.9 | 81 | |
| -0.5 | 45.5 | 82 |
شروط تعیینشده را به یاد آورید:
- در هر دور فقط یکبار کنترل را اندازهگیری میکنیم؛ فرض کنید که هر یک از دادههای بالا مربوط به یک دور است (البته این وضعیت ازنقطهنظر US CLIA واقعی نیست[2]، اما بنای ما بر آن است که از تعداد کم شروع کنیم.)
- از قانون R:4s استفاده نمیکنیم، زیرا در یک دور دو نتیجهی کنترل نداریم (داشتن دو نتیجه در یک دور تفسیر توصیهشده برای قانون R:4s است.)
- نقض قانون 2s را در نظر نمیگیریم. بیایید از همین حالا این عادت را ترک کنیم. درهرحال، من این دادهها را بهصورت تصادفی تهیه نکردهام، بنابراین انتظار نداریم شاهد تعداد معینی دادههای پرت 2s باشیم
- قصد داریم دادههای پرت در رابطه با این “قوانین وستگارد” را پیدا کنیم: 1:3s/2:2s/R:4s/4:1s/8:x (با این استثنا که قرار شد R:4s را به کار نبریم.)
- بنا نیست در باتلاق تکرار کنترلها گرفتار شویم. بنابراین فرض اینکه حتی یکی از دادههایی که میبینید حاصل تکرار کنترل است را از ذهن خود خارج کنید– توجه خود را فقط بر “درون” یا “بیرون” بودن دادهها معطوف کنید
نمودارها
گمان من بر این است که این دادهها برای بیشتر خوانندگان یک جدول بلندبالا به شمار میآید و شاید اندکی زیادهخواهی باشد اگر از خوانندگان بخواهم که دادهها را به چیزی مانند یک نمودار لوی– جننیگز تبدیل کنند؛ بنابراین برای کمک به خوانندگان دادهها را به تعدادی نمودار لوی– جنینگز تبدیل کردهایم
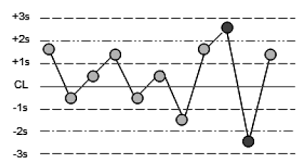
این 27 دادهی نخست است:
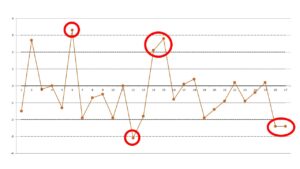
این بخش دوم دادههاست (از 32 تا 56):
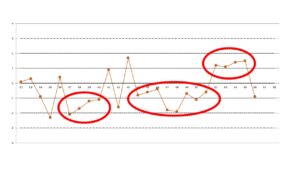
و این بخش انتهایی دادههاست (57 تا 82):
(بیگمان، دادههایی که در این نمودارها نمایش داده نشده است، پذیرفته بوده است.)
خوب، آیا شما هم همین موارد نقض قوانین را بر روی نمودارها نمایش نمایش داده شده است پیدا کردید؟ موارد نقض عبارت است از:
- 9 مورد نقض قوانین مختلف:
- 2 بار نقض قانون 1:3s
- 2 بار نقض قانون 2:2s
- 2 بار نقض قانون 4:1s
- 2 بار نقض قانون 8:x
- 1 بار نقض قانون 10:x
- اگر فقط “قوانین وستگارد” 1:3s/2:2s/R:4s برای این روش لازم بود:
- آنگاه 5 مورد از نقض قوانین شامل نقض 4:1s، 8:x، و 10:x اهمیت نداشت (بر اساس این رخدادها نتایج بیماران در آن دورها را مردود به شمار نمیآوردیم.)
- اگر فقط قانون پایش 1:3s برای این روش لازم بود:
- آنگاه 7 مورد از نقض قوانین شامل نقض 2:2s، 4:1s، 8:x، و 10:x اهمیت نداشت (بر اساس این رخدادها نتایج بیماران در آن دورها را مردود به شمار نمیآوردیم.)
افزودههای مترجم:
آقای میلاد فرزین از همدان پاسخ کامل به سؤالات بخش نخست را برای مجله ایمیل کردهاند که نشان از علاقهمندی و دقت فراوان ایشان دارد و بهدرستی نتیجه گرفتهاند که “درصورتیکه فقط از قانون 1:3s استفاده شود، پایش کیفیت سامانهی سنجش آسانتر خواهد بود.”نتیجهگیری ایشان، دقیقاً همان هدفی است که آقای استن وستگارد از نوشتن این سلسله مقالات دنبال میکند و تلاش دارد بهصورت گامبهگام خواننده را به اینسو راهنمایی کند که در همهی موارد نباید از “معیار چند قانونی وستگارد”[3] یعنی 1:3s/2:2s/R:4s/4:1s/8(or 10)x استفاده کرد، بلکه باید بسته به درجهی کیفیت روش مورداستفاده، از معیار مناسب برای پایش کیفیت استفاده کرد. هرچه کیفیت یک روش بهتر باشد، معیارهای سادهتری لازم است و نیز تعداد سنجش مادهی کنترل به ازای هر دور کمتر است، درنتیجه درحالیکه برای پایش روشهای خیلی خوب فقط یکبار سنجش مادهی کنترل در هر دور و به کار بستن قانون 1:3s کافی است، برای روشهایی که کیفیت پایینی دارند لازم است در هر دور 4 یا 6 بار مادهی کنترل را سنجید و با استفاده از معیار چند قانونی وستگارد آنها را پایش کرد.
انتخاب معیار مناسب برای پایش کیفیت با در نظر گرفتن ویژگیهای اجرایی روش (شامل عدم دقت و نامیزانی) و خطای کل مجاز، مطلبی است که پروفسور وستگارد از چند دهه پیش بر آن تأکید کرده است زیرا به گفتهی ایشان “هیچ معیار یگانهای برای پایش کیفیت وجود ندارد حتا قانون وستگارد!”
همکار بزرگوار دیگری، ضمن پاسخهای درستی که بهدفعات نقض قوانین دادهاند اضافه کردهاند “که در صورت در نظر نگرفتن قوانین 4:1s و 8:x، خطاهای سامانمند[4] تقریباً نادیده گرفته میشود و درصورتیکه بخواهیم فقط از قانون 1:3s استفاده کنیم فقط خطاهای تصادفی کشف میشود.”
پیش از پرداختن به نکتهای که ایشان مطرح کردهاند به نظرم توضیح کوتاهی در رابطه با استفاده از پایش کیفیت برای شناسایی خطاها میتواند راهگشا باشد؛ همانطور که میدانیم پیش از شروع به استفاده از یک روش برای سنجش نمونههای بیماران باید عملکرد آن را بررسی کرد و نامیزانی و عدم دقت آن را به دست آورد، سپس درصورتیکه نامیزانی و تکرارپذیری آن روش بهاندازهای باشد که خطای کل حاصل از آنها از خطای کل مجاز کوچکتر باشد میتوان از آن در آزمایشگاه استفاده کرد اما باید راهکاری اندیشید که در طی استفاده از آن روش، درصورتیکه نامیزانی یا عدم دقت ” افزایش یافت” مطلع شویم و آن را اصلاح کنیم؛ و این وظیفهای است که بر دوش برنامههای پایش کیفیت گذاشته شده است. حال با این توضیح برگردیم به نکتهی بالا.
اگرچه کاملاً درست است که قانون 1:3s حساسیت زیادی برای شناسایی افزایش خطای اتفاقی دارد اما این به آن معنا نیست که از این قانون نمیتوان برای شناسایی افزایش خطای سامانمند استفاده کرد. درواقع هیچیک از قوانین پایش کیفیت، برای شناسایی افزایش خطای سامانمند یا افرایش خطای تصادفی اختصاصی نیستند، بلکه برخی از آنها برای شناسایی افزایش عدم صحت حساسیت بیشتری دارند و برخی برای شناسایی افزایش CV حساسیت بیشتری دارند. پروفسور وستگارد و دیگران با استفاده از محاسبات آماری و شبیهسازی کامپیوتری، توانایی قوانین مختلف را برای شناسایی رخدادهای گوناگون شامل افزایش خطای سامانمند بهتنهایی، افزایش خطای تصادفی بهتنهایی، و افزایش همزمان هردو بررسی کردهاند که حاصل آن بررسیها بهصورت نمودارهایی با نام “منحنیهای توان”[5] یا “نمودارهای عملکرد توان”[6] منتشر شده است[7]. بر اساس نتایج این نمودارها، برخی قوانین برای پایش خطای سامانمند (منظم) و برخی برای پایش خطای تصادفی “مناسبتر” دانسته شدهاند.
امروزه و برای دستگاههای تمامخودکار امروزی فرض بر این است که خطای تصادفی تغییر نمیکند (یعنی در طول زمان CV تقریباً ثابت میماند) و باید توجه ما معطوف به شناسایی افزایش عدم صحت (یعنی تغییر کالیبراسیون) باشد (مثلاً به دنبال تغییر شماره ساخت کیتهای ایمونواسی، تعویض معرف، انجام برنامههای نگهداری دورهای یا تعویض قطعات دستگاه). بر اساس همین فرض است که شاهد هستیم نمودارهای توانی که در منابعی مانند کتابهای وستگارد و دستور کار [8]CLSI چاپ شدهاند، صرفاً برای شناسایی افزایش خطای سامانمند هستند و زیر محور افقی آنها نوشته شده است ∆SE. نکتهی جالبتوجه در این نمودارها این است که در آنها قوانینی مانند 1:3s یا 1:3.5s وجود دارد. بنابراین، اینکه نقض قانون 1:3s نشانهی خطای سامانمند است یا خطای تصادفی، بستگی به پیشفرضهای ما دارد. بهعنوان یک مثال مشابه، آزمایش HCG را در نظر بگیرید؛ اینکه افزایش HCG نشانهی بارداری است یا نشانهی بیماریهای تروفوبلاستیک، بستگی به وضعیتی دارد که این آزمایش را به کار میبریم: بهعبارتدیگر بستگی دارد به اینکه اندازهگیری hCG برای خانم جوانی انجام شده است که نشانههای مشکوک به بارداری دارد، یا برای خانم سالمندی است که نشانههای تومور سلولهای زایا دارد. تفسیر قانونی مثل 1:3s هم به همین شکل است؛ اگر برای روشی تمامخودکار استفاده شده است که تکرارپذیری آن پایدار است (یعنی اطمینان داریم که در طول زمان CV آن از مقدار اولیه بیشتر نمیشود) آنگاه نقض این قانون نشانهی افزایش خطای سامانمند (تغییر کالیبراسیون دستگاه) است. برعکس، اگر از روشهایی استفاده میکنیم که با هر دور کاری کالیبر میشوند اما خیلی در معرض عوامل نوسان هستند، نقض این قانون بیشتر میتواند نشانهی افزایش CV باشد.
در ادامهی مکاتبات با این همکار گرانقدر، ایشان پرسش زیر را مطرح فرمودهاند:
“اگر در یک دستگاه تمامخودکار امروزی که نوسان اندازهگیری پایینی دارد، کاربر دستگاه سرم کنترل را در حجم نادرستی از آب حل کند، یا پس از ذوب سرم کنترل آن را مخلوط ننماید، یا بستهی جدیدی از کیت را باز کند و بدون کالیبراسیون مجدد از آن استفاده کند، یا . . . و نتایج خارج از 3 برابر انحراف معیار به دست آورد، آیا این یک خطای تصادفی نیست؟”
در پاسخ به این پرسش:
الف) به نظر میرسد منظور این همکار از واژهی “تصادفی” در این پرسش “رخداد تصادفی” است نه خطای تصادفی. در پایش کیفیت وقتی گفته میشود یک قانون “خطای تصادفی” را شناسایی میکند منظور این است که وقتی CV از مقدار اولیه بیشتر شد آن قانون نقض میشود و به همین شکل وقتی گفته میشود یک قانون “خطای سامانمند” را شناسایی میکند منظور این است که وقتی کالیبراسیون روش به هم خورد و عدم صحت آن افزایش یافت آن قانون نقض میشود. اینکه کاربری بهطور تصادفی خطایی را به سامانهی سنجش وارد کند، یک رخداد تصادفی است که الزاماً سبب افزایش خطای تصادفی (یعنی افزایش CV) نمیشود، بهعنوانمثال، اگر “کاربر بستهی جدیدی از کیت را باز کند و بدون کالیبراسیون مجدد از آن استفاده کند” نتیجهی آن افزایش عدم صحت خواهد بود نه افزایش CV؛ یعنی به دلیل یک رخداد تصادفی، خطای سامانمند افزایش یافته است در حالی که خطای تصادفی (CV) همانند قبل باقی مانده است. برعکس، اگر کاربری بهطور تصادفی دوشاخهی سل کانتر را به پریزی وصل کند که به پایدارکنندهی جریان الکتریسیته متصل نیست، این رخداد تصادفی سبب افزایش خطای تصادفی (یعنی افزایشCV) خواهد شد.
ب) با توضیحی که در بالا آمد پیداست که اشتباه در تهیهی مادهی کنترل نیز یک رخداد تصادفی است نه افزایش خطای تصادفی. البته باید تا سرحد ممکن تلاش شود که چنین اشتباههایی رخ ندهد زیرا در صورت اشتباه در تهیهی مادهی کنترل، درحالیکه سامانهی سنجش بهدرستی کار میکند و خطاهای سامانمند و تصادفی همانند قبل است و هیچیک افزایش نیافته است، قوانین پایش کیفیت بهطور کاذب نقض میشوند و سبب اتلاف وقت و هزینه میشود (یکی از مزیتهای مواد کنترل آماده این است که از خطاهای آمادهسازی مصون هستند). برای اینکه مواد کنترل بهدرستی آماده شوند باید راهکارهای مناسب اندیشیده شود شامل تهیهی دستور کار و آموزش کاربران. همچنین یک راهکار برای پی بردن به چنین اشتباههایی این است که پیش از تمام شدن شیشهای که قبلاً آماده شده بوده است، شیشهی جدید آماده شود و همراه با مادهی رو به تمام شدن، خوانده شود و نتایج باهم مقایسه شود.
[1] z-score
[2] مترجم: بر اساس قوانین CLIA، آزمایشگاههای امریکا باید در هرروز دستکم 2 سطح کنترل را اندازهگیری کنند.
[3] Westgard Multi-rule
[4] Systematic errors
[5] Power Curves
[6] Power Function Graphs
[7] نمونهی خوبی از این بررسیها در منبع زیر منتشر شده است:
CIJN. CHEM. 23/10, 1857-1867 (1977)
CLINICAL CHEMISTRY, Vol. 23, No. 10, 1977 1857
James 0. Westgard, Torgny Groth, Torsten Aronsson, Hans Falk, and Carl-Henric de Verdler. Performance Characteristics of Rules for Internal Quality Control: Probabilities for False Rejection and Error Detection. Clin Chem 23/10, 1857-1867 (1977) .
- CLSI C24A3. Statistical quality control for quantitative measurement procedures. Clinical and Laboratory Standards Institute, Wayne PA, 2006.
همهی قوانین را نقض کنید! (بخش نخست)
پیشسنجش: سرچشمهی بیشتر خطاهای آزمایشگاهی؟!
برای دانلود پی دی اف بر روی لینک زیر کلیک کنید
ورود / ثبت نام