«خطای کل مجاز تعدیل شده» چیه؟!
نقدی به مفهوم «تعدیل خطای کل مجاز» به دنبال سنجش تکراری نمونهها، ارائه شده توی کتاب «مدیریت کیفیت در بیوشیمی» نوشته آقای دکتر رضا محمدی
حسن بیات؛ درسخونده علوم آزمایشگاهی
توضیح:
این نوشته با انشای گفتاری نوشته شده. قصد خاصی از اینطور نوشتن ندارم جز این که با نوشتن به این شکل هم مطلب رو راحتتر بیان میکنم و هم سریعتر مینویسم؛ که هر دو مورد، سبب صرفهجویی توی وقت کمی میشه که برای مطالعه و نوشتن دارم. از طرف دیگه، توی سالهای اخیر رد و بدل کردن پیامهای متنی با زبان گفتاری توی فضای مجازی سبب شده دیگه مطالعه مطالب به این شکل خیلی نامأنوس نباشه. به هر حال، از دستاندرکاران نشریه اخبار آزمایشگاهی خواهش کردم حداقل به عنوان یه تجربه، این نوشته به این شکل منتشر بشه.
مثالهای سادهای از فعالیتهای غیر آزمایشگاهی آوردم که به باور من به فهم مطلب کمک میکنه. از اونجایی که «اندازهگیری کمی» بخش عمدهای از کار آزمایشگاهه و محصول کار ما عمدتاً تولید «نتایج عددییه»، میشه به آزمایشگاه به چشم یه «کارگاه تولید نتایج کمی» نگاه کرد؛ و بنا بر این، میشه از مثالها و تشبیههایی از کارهای تولیدی و بخصوص مؤسسات اندازهگیری برای کمک به توضیح مباحث آزمایشگاهی استفاده کرد. امیدوارم مثالهای ارائه شده از جنس مثالهایی باشه که پروفسور وستگارد در بارهشون میگه «تو مثالهایی میزنی که از هر سدی در مقابل فهمیدن و یادگیری عبور میکنه». به هرحال، امیدوارم سادگی مثالها و همینطور سادهنویسی و مفصلنویسی من، سبب رنجش خوانندگان گرامی نشه.
توی فرمولهــــــایی که توی متن هســـــــت، علامت % رو نذاشتــــــم تا از شلوغ شدن فرمولها جلوگیری بشه؛
مثلاً %TAE = %Bias + 2CV به صورت TAE = Bias + CV نوشته شده. مطمئنا خوانندگان به خوبی آگاه هستن که کجاها باید به شکل درصد باشه؛ مثلاً این که هر جا توی فرمول CV هست، بقیه اجزا باید به شکل درصد باشه.
مقدمه
این نوشته، نقدییه به مفهومی با اسم «خطای کل مجازِ تعدیل شده» (Modified Allowable Total Error; mTEa) که توسط آقای دکتر رضا محمدی توی کتابشون با عنوان «مدیریت کیفیت در بیوشیمی» (نشر آییژ؛ سال 1395) ارائه شده. تو صفحه 56 کتاب، نویسنده مدعی شده اگه برای کوچیک کردن CV، نمونهها رو بیشتر از 1 بار اندازهگیری و میانگین نتایج رو گزارش بکنیم، اون وقت باید خطای کل مجاز (خکم) (Allowable Total Error, TEa) رو هم تعدیل، یا به عبارت بهتر، کم بکنیم. نویسنده یه فرمول هم برای این کار ابداع و ارائه کرده:
%mTEa = [(2+√n)/3√n]*TEa
این پیشنهاد به طور خلاصه این میشه که وقتی ما با عملکرد معمولمون، نمیتونیم درون محدوده مجاز باشیم و از حد مجاز رد میشیم، و بنا بر این با صرف تلاش بیشتر، هزینه بیشتر، و وقت بیشتر، عملکردمون رو بهتر میکنیم تا بیفتیم توی محدوده مجاز، همزمان باید حد مجاز هم برای ما کمتر بشه؛ کاری که امکان داره نه تنها پیامد بهتری به دنبال نداشته باشه و سبب نشه یه عملکرد بیرون از محدوده مجاز بیفته توی محدوده مجاز، حتا ممکنه سبب بشه یه عملکرد قابل قبول بیفته بیرون از محدوده مجاز و مردود بشه. قصد من از این نوشته اینه که نشون بدم همچین تعدیلی درست نیست.
خطای مجاز برای هر عملکردی تو هر سامانهای، از جمله خطای مجاز سنجشهای آزمایشگاهی، مقدار ثابتییه که با توجه به شرایط و نیازهای اون سامانه تعریف و تعیین میشه و تلاشهایی که برای بهبود عملکرد انجام میشه سبب نمیشه که خطای مجاز رو کم بکنیم. برای بیان موضوع، لازمه اول یه مرور کوتاه (البته نه خیلی کوتاه) داشته باشیم به بعضی از جنبههای مبحث پایش کیفیت (پک).
خطای مجاز «محصول» در مقابل خطای مجاز «تولید»
خطای مجاز «محصول» به ما میگه که یه دونه محصول، چه مشخصاتی باید داشته باشه تا اون رو خوب یا قابل قبول به حساب بیاریم. در مقابل، خطای مجاز «تولید» در باره مشخصات عملکرد خوب یا قابل قبول صحبت میکنه.
مثلاً اگه به یه تولیدکننده بگن خطای مجاز برای قطر توپهای بازی برابره با 20%، این میشه مشخصات یه دونه محصول خوب یا اختلاف مجاز. این خطای مجاز به ما میگه اگه مثلاً یه مشتری توپهایی با قطر 30 سانت بخواد (قطر هدف برابر 30)، تا 6 سانت کم و زیاد اشکال نداره و توپهایی به قطر 24 سانت تا 36 سانت، خوب، درست، سالم یا قابل قبول به حساب میآن و توپهایی که بیشتر از 6 سانت کم و زیاد دارن یعنی توپهایی با قطر کمتر از 24 سانت یا بیشتر از 36 سانت، بد، نادرست، ناسالم یا غیرِ قابل قبول به حساب میآن.
اما علاوه بر دونستن خطای مجاز محصول، لازمه یه تولیدکننده خطای مجاز تولید رو هم بدونه؛ یعنی بدونه چند درصد از توپهایی که تولید میکنه باید خوب باشن: همهشون (100%)؟ 95%؟ 70%؟ چند درصد؟ به بیان دیگه، قطر چند درصد از توپها باید بیفته توی محدوده مجاز 20%±30 (24 سانت تا 36 سانت). فرض کنیم توی قرارداد با یه توپساز، علاوه بر «اختلاف مجاز، برابره با 20%»، بنویسن «خطای مجاز تولید، برابره با 85%». این یعنی باید قطر حداقل 85% از توپها بیفته توی محدوده مجاز 20%±30؛ یا قطر حداکثر 15% از توپها میتونه بیفته بیرون از فاصله 20%±30. حالا تکلیف اون توپساز روشنه و میدونه که اگه یه سفارش 10000 تایی رو تحویل میده، باید قطر حداقل 8500 تا از توپها قابل قبول (یعنی از 24 تا 36) باشه. از اون طرف اگه قطر حداکثر 1500 تاشون نادرست باشه (بیفته بیرون از 24 تا 36)، اشکال نداره.
قرارداد بدی نیست چون این معیارها خیلی سخت به نظر نمیآن: (الف) خطای مجاز = 20%، (ب) خرابی مجاز = 15%. البته همه مشتریها خواستههای یکسان ندارن، ممکنه یه مشتری دیگه بیاد بگه ما 1000 تا توپ با قطر 20 سانت میخواهیم با معیارهای مثلاً «الزامات بهبود کیفیت فوتبال»: (الف) خطای مجاز = 5%، (ب) خرابی مجاز = 1%. از منظر نیازهای این مشتری، (الف) یه دونه محصول قابل قبول، توپییه که قطرش بین 21 تا 23 سانت باشه و (ب) تولید قابل قبول یعنی خیالش راحت باشه توی 1000 تا توپی که تحویل میگیره حداکثر 10 تا شون خرابه و حداقل 990 تاشون خوبه.
حالا «توپبازی» رو بذاریم کنار، ببخشید «توپسازی» رو، بریم سراغ چند تا مثال درباره «اندازهگیری» و «نتیجه اندازهگیری». کار اصلی ما آزمایشگاهیها اندازهگیرییه و مثل همه شغلهای مرتبط با اندازهگیری، متر کردن کوچهها باشه یا وزن کردن اشیا یا …، محصول ما میشه «نتیجه اندازهگیری» و تولید ما میشه «کار اندازهگیری»؛ به بیان بهتر: «نتیجه سنجش» و «عملکرد سنجشی».
«نتیجه سنجش» قابل قبول. به نتیجهای میگیم قابل قبول (درست یا خوب) که اختلاف اون با مقدار واقعی کمتر از مقدار مجاز باشه. اگه کار ما اندازهگیریها طول کوچههاس و به ما گفتن «اگه نتیجه اندازهگیریتون حداکثر 10% با اندازه واقعی اختلاف داشته باشه میگیم جوابتون خوبه (قابل قبوله)»، این میشه اختلاف مجاز، یا انحراف مجاز، یا خطای مجاز (یا هر اسم مناسب دیگه). حالا اگه ما بریم یه کوچه با طول واقعی 100 متر رو اندازه بگیریم، اختلاف مجاز واسه این طول این کوچه میشه 10 متر و محدوده مجاز نتایج میشه از 90 متر تا 110 متر:
10% * 100 = 10 m
100 – 10 = 90 m
100 + 10 = 110 m
تا وقتی که جوابمون تو فاصله 90 و 110 باشه، جوابمون یه محصول سالم به شمار میآد؛ یعنی درسته، خوبه، یا قابل قبوله؛ مثلاً اگه گزارش بکنیم 108 متر یا 91 متر، کنار جوابمون علامت «درست» میزنن؛ اما اگه گزارش بکنیم 111 متر یا 86 متر، علامت «نادرست» میزنن.
در مورد اندازهگیریهای آزمایشگاهی هم همینطوره. مثلاً با معیار CLIA، یه جواب گلوکز درست جوابییه که حداکثر 10% با مقدار واقعیش اختلاف داشته باشه. اگه مقدار واقعی گلوکز توی یه نمونه mg/dL 100 باشه، جوابهای بین 90 و 110 درست به حساب میآد و جوابهای بیرون از این محدوده، نادرست به حساب میآد.
«عملکرد سنجشی» قابل قبول. حالا فرض کنیم ما یه شرکت نقشهبرداری داریم و رفتیم با شهرداری یه شهر قراردار بستیم براشون کوچههای شهر رو متر کنیم. موقع قرارداد بستن باید ازشون بپرسیم: (الف) خطای مجاز چقدره؟ دستاندرکاران شهرداری هم بسته به کاربرد نتایج، تعیین میکنن که چقدر خطا براشون مهمه و اون رو توی قرارداد مینویسن؛ مثلاً همون 10% مثال بالا. اما حواسمون باید باشه که فقط دونستن خطای مجاز کافی نیست، بلکه باید در باره درصد مجاز خرابی هم بپرسیم: (ب) چند درصد از نتایج ما باید درست باشه؟ این پرسش یعنی: از نظر شما «عملکرد سنجشی» قابل قبول چه جور عملکردییه؟ معلوم کنین حداکثر چند درصد از نتایج ما میتونه بیفته بیرون از محدوده مجاز 10%±؟ فرض کنیم شهرداری توی قرارداد مینویسه 5%.
حالا تکلیف ما معلومه: اگه اون منطقه 10000 تا کوچه داره، برای این که آخر کار شهرداری پول ما رو بده باید طبق قرارداد، حداقل اندازه 9500 تا از کوچهها رو درست گزارش کرده باشیم (یعنی اندازه گزارش شده برای حداقل 9500 تا از کوچهها، بیشتر از 10% از مقدار واقعیشون کمتر یا بیشتر نباشه). با این معیار ما فقط 5% جای خطا داریم یعنی اندازه گزارش شده برای حداکثر 500 تا از کوچهها میتونه بیشتر از 10% از مقدار واقعیشون کوچیکتر یا بزرگتر باشه.
چرا دونستن خطای مجاز عملکرد مهمه؟ چون در عمل ما نمیخواهیم یا نمیتونیم تک تک محصولها رو وارسی کنیم ببینیم کدوم سالمه کدوم ناسالم. میخواهیم 1000 تا پرتقال بخریم، توی هر بسته پذیرایی یه دونه بذاریم بدیم دست شرکتکنندههای کنفرانس. نمیتونیم تک تک پرتقالها رو باز کنیم ببینم کدوم سالمه و کدوم ناسالم، تا ناسالمها رو دور بریزیم و سالمها رو بدیم دست مهمونها. اما اگه بدونیم پرتقالها مثلاً کمتر از 1% خرابی داره، میگیم «خرابی کل این بار کمه، میخریم میذاریم تو بستهها. اینجوری هر کسی باید حداقل 99% احتمال بده که پرتقالی که نصیبش شده سالمه و حداکثر 1% احتمال داره که خراب باشه».
توی آزمایشگاه هم داستان همینه؛ مثلاً وقتی یه اتوآنالایزر در ماه 5000 تا جواب گلوکز تولید میکنه، راهی نداریم که بدونیم کدوم جواب درسته و کدوم نادرست مگر این که مقادیر واقعی اون 5000 تا نتیجه رو بدونیم؛ که اگه میدونستیم دیگه نیازی نبود نمونهها رو بذاریم روی این اتوآنالایزر! تنها اطلاعاتی که میتونیم درباره درستی/نادرستی نتایج بدیم اینه که تعیین کنیم هر جواب چقدر احتمال داره درست باشه. همهمون میدونیم که احتمال رو میشه از روی فراوانی اون حساب کرد. اگه توی یه کیسه 100 تا توپ باشه که فقط 95 تاشون سالم باشه، احتمال این که توپی که به طور تصادفی از کیسه در میاریم سالم باشه برابره با 95%.
اگه یه خط تولید داشته باشیم که حداقل 95% از تولیدش خوب باشه، احتمال خوب بودن هر محصول برابره با حداقل 95%. به همین شکل، اگه یه اتوآنالایز داشته باشیم که حداقل 95% از جوابهای گلوکزش کمتر از 10% با مقدار واقعی اختلاف داشته باشن، احتمال این که هر جواب کمتر از 10% با مقدار واقعی اختلاف داشته باشه برابره با حداقل 95%.
اینجاس که ارزیابی عملکرد سنجشی و اطمینان از پذیرفته بودن اون اهمیت پیدا میکنه. در مثال اندازهگیریهای کوچهها، اگه عملکرد سنجشی ما قابل قبول باشه، اون وقت کاربر نتایج در مورد طول هر کوچه، حداقل 95% مطمئنه که حداکثر 10% از مقدار واقعی کمتره یا بیشتره. مثلاً اگه بخش عمرانی شهرداری بخواد کوچههای اون شهر رو سنگفرش بکنه و از ما بپرسه که توی حساب کتابشون بر اساس نتایجی که ما گزارش کردیم، چقدر خطا رو باید در نظر بگیرن (یا به قول مهندسهای عمران، چند درصد تولرانس در نظر بگیرن) میتونیم توضیح بدیم «طول این کوچهها با خطای مجاز 10% اندازهگیری شده، پس شما حداکثر 10% کم و زیاد رو در نظر بگیرین».
بعد میپرسن: «یعنی خیالمون صد درصد راحت باشه در مورد هیچ کوچهای بیشتر از 10% کم و زیاد نداریم؟» ما هم جواب میدیم: «صد درصد که نه! خیالتون حداقل 95% راحت باشه»؛ یعنی حداقل توی 95% از کوچهها، حساب کتابتون درست از کار درمیاد اما توی حداکثر 5% از کوچهها، با بیشتر از 10% کم و زیاد روبرو میشین. کدوم کوچهها خطاشون از 10% بیشتره؟! (کدوم پرتقالها خرابه؟!) نمیدونیم! به خاطر همینه که میگیم به محاسباتتون برای هر کوچه، حداقل 95% اطمینان داشته باشین. اگه این کیفیت سنجشی برای تصمیمات عمرانیتون مناسبه، با ما قرارداد ببندین کوچهها رو اندازهگیری کنیم.
در مورد اندازهگیریهای آزمایشگاهی هم همینطوره؛ یعنی هم لازمه بدونیم اختلاف مجاز واسه هر نتیجه چقدره و هم این که بدونیم چند درصد از جوابهای ما میتونه نادرست باشه (بیفته بیرون از محدوده مجاز). مورد اول، یعنی اختلاف مجاز رو به شکل سرراست خیلی جاها نوشتن. توی جدولهای خطای مجاز CLIA و RCPA میشه خطاهای مجاز برای سنجش خیلی از آنالیتها رو پیدا کرد؛ برای بعضیهاشون به شکل درصد نوشتن (مثلاً CLIA خطای مجاز کلسترول رو 10% در نظر گرفته) و برای بعضیهاشون به شکل یه مقدار ثابت نوشتن (باز هم مثلاً CLIA خطای مجاز کلسیم رو mg/dL 1 در نظر گرفته).
اما در مورد دومی، یعنی این که درصد مجاز جوابهای نادرست چقدره، راستش رو بخواهین جایی به شکل سرراست چیزی ننوشتن. از حدود 50 سال پیش که پروفسور وستگارد مدل خطای کل رو ارائه کرده، یه جور توافق نانوشته بوده که اجازه داریم حداکثر 5% از جوابهامون بیفته بیرون از محدوده مجاز (یعنی درصد مجاز خرابی یا تولید خطا یا هر اصطلاح مناسب دیگه، برابره با 5%).
مثال: فرض کنیم واسه سنجش گلوکز، اختلاف مجاز رو برابر 10% و درصد مجاز خرابی رو برابر 5% درصد در نظر گرفتیم و با یه مرکز قرارداد بستیم گلوکز 10000 تا از کارکنانش رو اندازهگیری کنیم. طبق این الزامات، برای این که عملکردمون قابل قبول باشه (و آخر کار پولمون رو بدن) باید حداقل 9500 تا از جوابهامون درست باشه، یعنی از مقدار واقعی، حداکثر 10% کمتر یا بیشتر باشن (یا حداکثر 500 تا از جوابهامون بیفته بیرون از محدوده مجاز 10%±). اگه عملکرد سنجشی آزمایشگاه در مورد گلوکز خوب باشه و کمتر از 5% جوابهامون نادرست داشته باشه، میتونیم به یه پزشک در مورد کیفیت کارمون اینجوری توضیح بدیم: «حداقل 95% از نتایج گلوکز ما درست هستن یعنی حداکثر 10% از مقدار واقعیشون کمتر یا بیشتر هستن و حداکثر 5% از جوابها نادرست هستن و بیشتر از 10% خطا (اختلاف) دارن».
کدوم نتیجهها بیشتر از 10% خطا داره؟ (کدوم پرتقالها خرابه؟ اندازه کدوم کوچهها بیشتر از 10% خطا داره؟) نمیدونیم! به خاطر همینه که میگیم در مورد هر جواب گلوکزی که از آزمایشگاه ما به دستتون میرسه، حداقل 95% اطمینان داشته باشین که دیگه خیلی… خیلی… خیلی… خطا داشته باشه، حداکثر 10% از مقدار واقعیش کمتره یا بیشتره. اگه این کیفیت رو واسه تصمیمات بالینیتون مناسب میدونین، مریضهاتون رو بفرستین آزمایشگاه ما.
اما…، چجوری تعیین کنیم که چند درصد از نتایج ما درسته؟ در مورد مثال اندازهگیری کوچهها، یه راه غیرعاقلانه اینه که شهرداری اندازه واقعی اون 10000 تا کوچه رو با یه ابزار اندازهگیری مرجع تعیین بکنه؛ تکتک اندازههای ما رو با اندازههای واقعی مقایسه بکنه و ببینه هر کدوم چند درصد اختلاف داره؛ اونهایی رو که بیشتر از 10% اختلاف دارن بشماره و حساب کنه چند درصد از جوابهای ما درسته؛ و بعد تصمیم بگیره که عملکرد ما درسته یا نه (و این که دستمزد ما رو بده یا نه). این راه غیرعاقلانهس چون اگه شهرداری اندازه واقعی کوچهها رو داشت که دیگه نیازی به قرارداد با شرکت ما نداشت.
همینطور در مورد اندازهگیری گلوکز، واسه بررسی این که عملکرد سنجشی ما خوبه یا بد، نمیشه مثلاً همه جوابهای گلوکز اون 10000 تا کارمند رو با مقدار واقعیشون مقایسه کرد تا معلوم بشه چند درصد از جوابهای ما درسته و چند درصد نادرسته. پس چی کار کنیم؟ اینجاس که محاسبه «خطای سنجشی کل؛ خسک» (Total Analytical Error; TAE) به کارمون میآد.
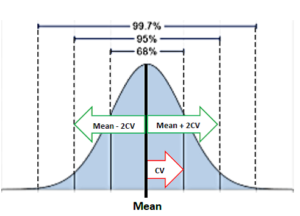
خطای سنجشی کل. بدون وارد شدن تو جزئیات، اگه عدم صحت و عدم دقت (Bias و CV) رو داشته باشیم، میتونیم به راحتی تعیین بکنیم که چند درصد از نتایج میافته توی محدوده خطای مجاز. حتا این هم لازم نیست که تعیین کنیم دقیقاً چند درصد توی محدوده مجازه، فقط کافیه معلوم کنیم آیا حداقل 95% درصد از نتایج میافته داخل محدوده مجاز یا نه. همونطور که میدونیم، بر اساس توزیع گوسی شکل (توزیع طبیعی)، 95% از سطح میانی زیر منحنی میافته توی فاصله 1.96*SD کمتر از میانگین تا 1.96*SD بیشتر از میانگین (یا 1.96*CV کمتر و بیشتر از میانگین). البته برای راحتی، از 2 به جای 1.96 استفاده میکنیم (شکل زیر).
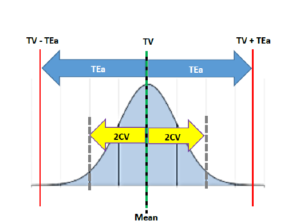
اگه Bias و CV طوری باشه که حداقل 95% از سطح زیر منحنی بیفته توی محدوده مجاز، عملکرد سنجشی ما پذیرفتهس. توی شکل زیر، میانگین سنجش کاملاً با مقدار هدف (True Value; TV) برابره و بنا بر این عدم صحت یا Bias برابر صفره.
Bias = Mean – TV = 0
همونطور که تو شکل زیر دیده میشه، چون CV از نصف TEa کمتره، بنا بر این Mean ± 2CV که 95% از نتایج رو در بر میگیره افتاده داخل TV ± TEa و این یعنی حداقل 95% از نتایج درسته.
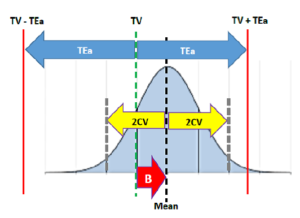
شکل بعدی حالتی را نشون میده که به رغم وجود مقداری عدم صحت (Bias)باز هم چون CV به اندازه کافی کوچیکه، Mean ± 2CV افتاده توی TV ± TEa و در نتیجه حداقل 95% از نتایج داخل محدوده مجازه و درست به حساب میاد (توی شکل زیر Bias با پیکان قرمز رنگ با حرف B مشخص شده).
Mean – TV│ > 0│
Bias│ > 0 │
این دو تا شکل چیزی رو که نشون میدن که همهمون به خوبی میدونستیم: تا وقتی که B + 2CV کوچیکتر از اختلاف مجاز بشه، میتونیم مطمئن باشیم که حداقل 95% از نتایج میافتن توی محدوده مجاز و درست هستن؛ و بنا بر این، عملکرد سنجشی خوبه یا قابل قبــــــــــوله. این مفهوم، اســـــــاس مدل «خطای کل» پروفسور وستگارده. توی این مـــــــدل، حاصل جمع B| + 2CV| رو میگـــــــــــن «خطای سنجشی کل» (Total Analytical Error; TAE):
TAE = |Bias| + 2CV
و اختلاف مجاز (همون ارقامی که توی جداولی مثل CLIA و RCPA و غیره هست) رو میگن «خطای کل مجاز» (Allowable Total Error; TEa). با این حساب اگه Bias|+ 2CV ≤ TEa| باشه یا به طور خلاصهتر TAE ≤ TEa باشه، اون وقت عملکرد سنجشی قابل قبوله؛ چون درصد جوابهای قابل قبولمون 95% یا بیشتره و درصد خطامون 5% یا کمتره.
وقتی سر و کارمون با یه دونه نتیجهاس، حداکثر اختلاف قابل قبول با مقدار واقعیش رو میگیم «اختلاف مجاز» یا «انحراف مجاز» یا «خطای مجاز» یا هر اصطلاح مناسب دیگهای که این مفهوم رو برسونه. مثلاً CLIA تو جداول قبلیش میگفت «اختلاف مجاز» (Acceptable Performance) اما توی جدول پیشنهادی 2019 میگه «حدود قابـــــل قبول» (Acceptable Limits)؛ CAP میگه «بازه قابل قبول» (Acceptable Range)؛ RCPA میگه «خطای مجاز» (Allowable Error)؛ و جدول RiliBak آلمان میگه «انحراف قابل قبول» (Acceptable Deviation)؛ منظور همهشون هم اینه که در مورد یه دونه نتیجه آزمایش، چقدر اختلاف با مقدار واقعی قابل قبوله. توی مدل خطای کل، چون قراره حساب کنیم به خاطر تأثیرات Bias و CV با هم، چند درصد از جوابهامون نادرست به حساب میان، به همین «اختلاف مجاز» میگن «خطای کل مجاز».
خطای سنجشی کل برای «یه دونه» جواب یا برای «عملکرد»؟
چون مدل خطای کل، روی قابل قبول بودن «عملکرد» تمرکز داره نه تک-جوابها، بنا بر این توی این مدل اصطلاح «خطای سنجشی کل» اساساً برای عملکرد استفاده میشه، نه تک-جوابها. چون همونطور که گفتیم قرار نیست ما بررسی کنیم هر کدوم از جوابها چقدر با مقدار واقعی اختلاف دارن. با استفاده از این مدل، بر اساس Bias و CV معلوم میکنیم آیا حداقل 95% از نتایج درست هست یا نه تا بدونیم آیا میشه به هر تک-جواب حداقل 95% اطمینان کرد که اختلافش با مقدار واقعی کمتر از خطای مجازه. به کار بردن واژه «کل» توی این مدل برای همین بوده که بگن به جای تمرکز روی تأثیر هر کدوم از Bias و CV به تنهایی، تمرکز گذاشته شده روی «کل» خطایی که Bias و CV با هم ایجاد میکنن.
البته اصطلاح «خطای سنجشی کل» برای اختلاف یه تک-جواب با مقدار واقعی هم به کار برده میشه؛ به این معنی که اختلاف با مقدار واقعی ناشییه از تأثیر کل Bias و CV روی هم؛ و البته تأثیر خطاهای پیشسنجش، مداخلهگرها و گاهی هم پسسنجش رو هم باید در نظر گرفت. به هر حال، باید یادمون بمونه که توی آزمایشگاه در مورد درستی/نادرستی تک-جوابها قضاوت نمیکنیم، بلکه تمرکزمون روی درستی/نادرستی عملکرده و مدل خطای کل در این مورد به کارمون میآد.
تکرار سنجش برای کاهش CV
اگه جمعیتی با توزیع گوسی داشته باشیم، با تعداد اعضای N، میانگین µ و انحراف معیار σ و از اون جمعیت تمام نمونههای n تایی ممکن رو بگیریم، توزیع اون نمونههای n تایی هم گوسی میشه، میانگینش X̄، برابر با میانگین جمعیت میشه، و انحراف معیارش، SD، برابر با n√/σ میشه.
X̄ = µ
SD = σ/√n
مثلاً اگه از یه جمعیت 1000 تایی با میانگین 50 و انحراف معیار 5، همه نمونههای 2 تایی ممکن رو بگیریم، میانگین و انحراف معیار توزیع نمونههای 2 تایی به ترتیب میشه 50 و 3.54:
X̄ = µ = 50
SD = σ/√n = 5/√2 = 3.54
و اگه همه نمونههای 10تایی رو بگیریم، میانگین و انحراف معیار توزیع نمونههای 10 تایی به ترتیب میشه 50 و 1.58:
X̄ = µ = 50
SD = σ/√n = 5/√10 = 1.58
همونطور که میبینیم، انحراف معیار توزیع نمونههای n تایی از انحراف معیار جمعیت کوچیکتره؛ هر چی n بزرگتر، انحراف معیار توزیع نمونه کوچیکتر. موقع بررسیهای آماری، برای این که یافتههای حاصل از نمونه، برآورد قابل اطمینانی از جمعیت باشه، لازمه n به اندازه کافی بزرگ باشه. در صورتی که n به اندازه کافی بزرگ باشه، میشه یافتههای آماری نمونه رو با اطمینان بالایی به جمعیت تعمیم داد و در باره جمعیت قضاوت کرد.
مثلاً اگه برای برآورد میانگین وزن یه جمعیت 10000 نفری از بچههای 10 ساله، فقط 1 بچه رو وزن کنیم و وزن اون بشه 27 کیلوگرم، مطمئناً نمیتونیم با اطمینان بگیم وزن متوسط این 10000 تا بچه تقریباً 27 کیلوگرمه؛ اما اگه 50 تا بچه رو وزن کرده باشیم و میانگین 27 رو به دست آورده باشیم، با اطمنیان بیشتری میتونیم بگیم وزن متوسط اون جمعیت حدود 27 کیلوگرمه؛ و اگه میانگین وزن یه نمونه 500 تایی 27 شده باشه، با اطمینان خیلی بیشتری میتونیم میانگین وزن جمعیت رو حدود 27 در نظر بگیریم.
از این موضوع که با افزایش n، انحراف معیار یا CV توزیع کوچیکتر میشه، میتونیم برای کاهش CV تو اندازهگیریها استفاده بکنیم. مثلاً اگه یه ترازو داشته باشیم که CV اون برای کارمون زیاد باشه، میتونیم برای کاهش CV، به جای 1 بار وزن کردن اشیا، هر چیز رو چند بار (n بار) وزن کنیم و از n تا نتیجه به دست اومده میانگین بگیریم. اگه CV ترازوی ما 15% باشه و هر چیز رو 5 بار وزن کنیم و میانگین بگیریم، CV اندازهگیریهای 5 تایی برابر 6.7% میشه. اگه CV نتایج تکراری رو با CVrepeat نشون بدیم:
CVrepeat = CV/√n = 15/√5 = 6.7%
اگه 6.7% هم برای کارمون زیاد باشه میتونیم تکرار رو بیشتر بکنیم، مثلاً 20 بار:
CVrepeat = 15/√20 = 3.5%
در مورد اندازهگیریهای آزمایشگاهی هم همینطوره. مثلاً اگه یه روش سنجش کراتینین داشته باشیم که CV اون 5% باشه و به جای 1 بار سنجش، نمونهها رو 2 یا 3 بار اندازهگیری کنیم و میانگین بگیریم، CV روش ما به ترتیب به 3.5% و 2.9% کاهش پیدا میکنه:
- CV حاصل از 2 بار سنجش: CVrepeat = 5/√2 = 3.5%
- CV حاصل از 3 بار سنجش: CVrepeat = 5/√3 = 2.9
اگه عدم صحت این روش برابر 1% باشه، خطای سنجشی کل میشه:
- 1 بار سنجش:TAE = 1% + (2 x 5%) = 11% %
- 2 بار سنجش: TAE = 1% + (2 x 3.5%) = 8% %
- 3 بار سنجش:%TAE = 1% + (2 x 2.9%) = 6.8 %
همونطور که در مثال بالا میبینینم، با سنجش تکراری، CV و در نتیجه TAE کم میشه.
عدم صحت مجاز، عدم دقت مجاز
تو مدل خطای کل، چیزی به اسم عدم صحت مجاز یا عدم دقت مجاز نداریم. داستان اینه که تا اواسط دهه 70 میلادی، مفهومی به اسم خطای کل سنجش مطرح نشده بود و صحبتی از این نبود که عدم صحت و عدم دقت روی هم چه نقشی در تولید نتایج خطا بازی میکنن. سال 1974، پروفسور وستگارد با 3 نفر از همکارانش، یه مقاله به کنفرانس AACC ارائه کردن و برای اولین مفهوم «خطای کل» رو (که حالا به اون میگیم «خطای سنجشی کل») معرفی کردن. بحث وستگارد و همکارانش این بود که به جای این که عدم صحت و عدم دقت رو به طور جداگانه بررسی کنیم، بیائیم «کل» خطای ناشی از Bias و CV با هم رو در نظر بگیریــــــم (به صورت TAE = B + 2CV).
ایده خطای سنجشی کل کمکم جا افتاد و تو کنفرانس AACC سال 1976 به عنوان شیوه ارزیابی و پایش کیفیت توی امریکا پذیرفته شد. از اون موقع تا حالا، علاوه بر امریکا، تو کشورهای دیگه مثل آلمان و استرالیا و البته کشور خودمون از این مدل استفاده میشه. البته خیلی از کشورهای اروپایی از مدل خطای کل استفاده نمیکنن و همچنان عدم صحت و عدم دقت رو به صورت جداگانه در نظر میگیرن و برای اونها «عدم صحت مجاز» و «عدم دقت مجاز» تعیین میکنن.
توی مدل خطای کل کاری ندارن به این که CV چقدره یا Bias چقدره، بلکه مهم اینه که خطای ناشی از ترکیب این دو تا با هم، یعنی «خطای سنجشی کل»، چقدره و این که «خطای سنجشی کل» از «خطای کل مجاز» بیشتر نشه تا مطمئن بشیم که بیشتر از 5% خطا تولید نمیکنیم. توی این مدل، انواع ترکیبهای عدم صحت و عدم دقت قابل تصوره؛ یه آزمایشگاه ممکنه عدم صحتش بزرگ باشه اما عدم دقتش کوچیک باشه؛ یکی دیگه برعکس، ممکنه عدم دقتش بزرگ باشه اما عدم صحتش کوچیک باشه؛ در مورد یکی دیگه ممکنه هر دو تا متوسط باشه و غیره.
اصلاً مهم نیست Bias و CV هر کدوم به تنهایی چقدر هستن؛ چیزی که مهمه اینه که کل درصد جوابهای نادرست که ناشی از Bias و CV روی همه، بیشتر از 5% نشه. به همین دلیل، توی منابع مربوط به مدل خطای کل مثل CLIA، CAP و RCPA و غیره چیزی به عنوان CV مجاز یا Bias مجاز ارائه نشده و فقط خطای کل مجاز (با اسامی مختلف) ارائه شده.
خطای کل مجاز مثل یه بودجه ثابته، مثلاً یه اعتبار خرید صد هزار تومنی که برای ما در نظر گرفتن بریم سیب و پرتقال بخریم. اینجا، «صورتحساب کل خرید سیب و پرتقال روی هم»، معادل خطای سنجشی کله؛ و «اعتبار صد هزارتومنی» معادل خطای کل مجازه (بگیم «خرید کل» و «خرید کل مجاز»). گفتن برین واسه خودتون تا سقف صد هزار تومن سیب و/یا پرتقال بخرین؛ کاری ندارن از هر کدوم چقدر میخریم، فقط مهمه که خرید کل ما از خرید کل مجاز بیشتر نشه.
یه نفر ممکنه بیشتر پرتقال بخره؛ یکی دیگه ممکنه برعکس عمل بکنه؛ یکی ممکنه فقط پرتقال بخره؛ یکی دیگه برعکس؛ یکی ممکنه ته صد هزار تومن رو دربیاره؛ یکی ممکنه متعادلتر خرید بکنه؛ یکی هم ممکنه صورتحسابش روی هم خیلی کم بشه و غیره. هر ترکیبی قابل قبوله به شرط این که وقتی میریم پای صندوق، صورتحسابمون حداکثر صد هزار تومن بشه. به همین شکل، توی مدل خطای کل هر ترکیبی از Bias و CV قابل قبوله به شرط این که خطای سنجشی کل (TAE) از خطای کل مجاز (TEa) بیشتر نشه.
سؤال: پس چرا میگن موقع ارزشیابی، CV بیست روزه نباید از 1/3خطای کل مجاز بیشتر بشه؟
قبل از توضیح در باره این، لازمه به این نکته توجه کنیم که نمیشه همه فضای TEa رو به CV و Bias اختصاص بدیم (یعنی نمیشه B + 2CV میزون اندازه TEa بشه). چون در اون صورت، دیگه فضایی برای پایش کیفیت (پک) باقی نمیمونه. واسه این که نریم تو جزئیات، یه مثال ساده رو در نظر بگیریم: اگه یه ظرف 1 لیتری داشته باشیم (یعنی TEa برابر 1 لیتر) مطمئناً میزون 1 لیتر شیر (یعنی TAE برابر 1 لیتر) نمیریزیم تو اون گرم کنیم، چون در اون صورت دیگه هیچ فضای خالیای نمیمونه که ما بتونیم سر نرفتن شیر رو «پایش» بکنیم.
باید یه مقدار از حجم 1 لیتری ظرف رو بذاریم واسه پایش؛ هر چی فضای باقیمونده بیشتر باشه، خیال ما راحتتره و سادهتر پایش میکنیم. تو آزمایشگاه هم همین طوره: هرچه CV و Bias کوچیکتر باشن، TAE از TEa کوچیکتر میشه و بنا بر این فضای بیشتری واسه پک باقی میمونه و در نتیجه میشه از یه برنامه پک سادهتر با هزینهتر و زحمت کمتر استفاده کرد. این موضوع رو میشه با رابطه زیر نشون داد:
TAE + QC = TEa
رابطه بالا تأکید میکنه که از فضای TEa، یه سهمی هم واسه پک لازمه (یه بخش از ظرف TEa رو خالی بذاریم واسه پایش سر نرفتن خطا!). با در نظر داشتن این موضوع، بریم سراغ این که اگه CV بیشتر از 1/3 خطای کل مجاز بشه چطور میشه. اگه CV برابر 1/3 خطای کل مجاز بشه:
TAE = B + 2CV
TAE = B + (2 x 1/3TEa)
TAE = B + 2/3TEa
و در بهترین حالت، اگه Bias برابر صفر بشه:
TAE = 0 + 2/3TEa
TAE = 2/3TEa
در این صورت، با در نظر گرفتن سهم پک:
TAE + QC = TEa
2/3TEa + QC = TEa
QC = 1/3TEa
یعنی با یه CV برابر 1/3 خطای کل مجاز و Bias برابر صفر،2/3 از فضای TEa به TAE اختصاص پیدا میکنه و فقط 1/3 از فضای TEa واسه پک باقی میمونه. با این فضای کم، باید از یه برنامه پک چندقانونی با حداقل 4 تا کنترل توی هر دور استفاده کرد که خیلی پرزحمت و پرهزینهس. حالا فرض کنیم CV از 1/3 خکم بیشتر باشه و/یا کمی هم Bias داشته باشیم؛ اون وقت فضای خیلی کمتری میمونه واسه پک و هزینه و زحمت خیلی بیشتری میمونه واسه ما.
البته به طور نظری، اگه یه روش داشته باشیم که کاملاً پایدار باشه طوری که مطمئن باشیم در طول مدتی که از اون استفاده میکنیم هرگز پایداریش به هم نمیخوره، اون وقت دیگه به پک نیازی نیست و میشه همه فضای TEa رو به TAE اختصاص داد. با همچین روش همیشه-پایدار و البته یافت ناشدنیای، اگه از قضا عدم صحت هم برابر صفر بشه، دیگه شانس CV زده و همه فضای TEa میمونه واسه اون. در این صورت، CV میتونه تا اندازه نصف TEa بزرگ باشه:
TAE + QC = TEa
(B + 2CV) + QC = TEa
(0 + 2CV) + 0 = TEa
CV = 1/2TEa
به همین شکل، اگه به طور نظری یه روش هم همیشه-پایدار با CV برابر صفر داشته باشیم، اون وقت همه TEa میمونه واسه Bias و عدم صحت میتونه تا اندازه TEa بزرگ باشه:
TAE + QC = TEa
(B + 2CV) + QC = TEa
(B + 2*0) + 0 = TEa
B = TEa
از اونجایی که در عمل همچین روشهای همیشه-پایداری نداریم و بنا بر این همیشه به پک احتیاج داریم، پس موقع ارزشیابی باید مطمئن باشیم که یه سهمی از فضای TEa میمونه واسه پک. واسه همینه که موقع ارزشیابی میگن CV از 1/3 فضای TEa بزرگتر نشه به این امید که Bias هم صفر یا خیلی کوچیک از کار درمیآد و حداقل نزدیک به یک سوم از TEa میمونه واسه پک. این به معنای این نیست که CV مجاز برابره با TEa1/3 و یا Bias مجاز برابره با TEa1/3.
یه سؤال دیگه: پس چرا تو جدول خطاهای مجاز بیولوژیک، هم TEa داریم هم CV مجاز و هم Bias مجاز؟
اول یادآوری نشانهها: توی جدول خطاهای بیولوژیک، CV مجاز و Bias مجاز و خطای کل مجاز به ترتیب با علائم I(%)، B(%) و TE(%) نشون داده شده.
همونطور که قبلاً گفته شد، I(%) و B(%) برای استفاده تو بعضی کشورهای اروپایییه که مقادیر CV و Bias رو به طور جداگانه ارزیابی و پایش میکنن و کاری هم به خطای سنجشی کل ندارن. اما استفاده از خطاهای مجاز جداگانه وقتی میرسه به برنامه پایش کیفیت خارجی (پکخ) با یه اشکال روبرو میشه. روش پکخ تو اون کشورها اینه که تو هر دوره، نمونههایی رو با مقدار هدف مشخص میفرستن آزمایشگاه (معمولاً مقدار هدف رو با روشهای مرجع تعیین میکنن). آزمایشگاه هم هر آنالیت رو 1 بار آزمایش میکنه و جواب رو برمیگردونه.
مشکل اینجاس که با یه تک-جواب نمیشه Bias و CV آزمایشگاه رو حساب کرد تا معلوم بشه که از B(%) و I(%) بزرگترن یا نه تا بشه در مورد عملکرد آزمایشگاه توی اون دوره تصمیم گرفت. البته عملی هم نیست که از آزمایشگاهها بخوان که تو هر دوره، ماده کنترل رو واسه هر آنالیت، مثلاً 20 بار اندازه بگیرن تا مجری پکخ بتونه CV و Bias اونها رو محاسبه و بررسی بکنه. واسه حل این مشکل، پروفسور فریزر و پروفسور پترسن[1] یه راهکار ارائه دادن با این استدلال که حالا مجریهای پکخ فقط به یه تک-جواب از آزمایشگاه محدود هستن بیائیم یه «حد مجاز اختلاف با مقدار هدف» تعیین کنیم با اسم TE(%) که مجریهای پکخ بتونن تک-جواب آزمایشگاه رو با اون مقایسه بکنن.
تصمیم هم گرفتن مقدار TE(%) به اندازهای باشه که اگه یه آزمایشگاه با Bias برابر با B(%) و CV برابر با I(%) کار میکنه (یعنی با حداکثر مقادیر مجاز واسه Bias و CV)، 95% احتمال داشته باشه که جوابش بیفته توی محدوده خطای مجاز و فقط 5% احتمال داشته باشه که جوابش به طور کاذب بیفته بیرون از محدوده خطای مجاز. البته هر چی Bias و CV آزمایشگاه از B(%) و I(%) کوچیکتر باشه، احتمال این که جوابش به طور کاذب بیفته بیرون از محدوده مجاز از 5% کمتر میشه. با این استدلال، اونها فرمول زیر رو واسه محاسبه «حداکثر اختلاف مجاز» برای استفاده توی برنامههای پکخ پیشنهاد کردن:
TE(%) = B(%) + 1.65*I(%)
اگه اختلاف جواب آزمایشگاه با مقدار هدف، TV، بیشتر از TE(%) باشه جواب آزمایشگاه رد میشه. بنا بر این، محدوده پذیرش میشه:
Acceptable Range = TV ± TE(%)
مثلاً توی جدول بیولوژیک 2014، B(%) برای گلوکز برابره با 2.34% و I(%) برابره با 2.8%. با این مقادیر، TE(%) میشه 6.96%:
TE(%) = 2.34% + 1.65*2.8% = 6.96%
Acceptable Range = TV ± 6.96%
اگه یه نمونه گلوکز با مقدار واقعی 100 رو بفرستن واسه آزمایشگاهها:
Acceptable Range = 100 ± 6.96%
Acceptable Range: From 93 to 107
انتظار دارن جواب آزمایشگاهها بیفته تو محدوده 6.96%±100؛ یعنی از 93 تا 107. حالا اگه یه آزمایشگاه با Bias برابر 2.34% و CV برابر 2.8% یعنی دقیقاً برابر B(%) و I(%) کار بکنه، 95% احتمال داره جوابش بیفته توی محدوده قابل قبول و 5% احتمال داره که جوابش بیفته بیرون از محدوده قابل قبول. همونطور که گفته شد، بیرون افتادن جواب این آزمایشگاه «رد کاذب» (False Rejection) یا «مثبت کاذب» به حساب میآد؛ اما مثل هر برنامه پایش دیگهای، برای این که حساسیت خطایابی خیلی کم نشه، باید مقداری رد کاذب رو تحمل کرد.
یکی از انتقادهای بجایی که به این پیشنهاد وارد شده اینه که ممکنه Bias یه آزمایشگاه بزرگتر از B(%) باشه اما CV اون به اندازهای کوچیکتر از I(%) باشه که جوابش از محدوده TV ± TE(%) بیرون نیفته؛ یا برعکس، CV آزمایشگاه بزرگتر از I(%) باشه اما Bias اون به اندازهای کوچیکتر از B(%) باشه که جوابش بیرون نیفته. به عبارت دیگه یه Bias بزرگتر از B(%) با یه CV کوچیک جبران بشه و برعکس. یادمون بیاد که- بر خلاف «مدل خطای کل» که اندازه Bias و CV به تنهایی مهم نیست بلکه تأثیر مشترک اونها به صورت TAE اهمیت داره- توی مدل «خطاهای مجاز جداگانه برای Bias و CV»، باید هم Bias از B(%) بزرگتر نباشه و هم CV از I(%) بزرگتر نباشه.
بنا بر این، اگه یکی از Bias یا CV بزرگتر از مقدار مجاز باشه اما توسط کوچیک بودن اون یکی جبران بشه طوری که جواب آزمایشگاه نیفته بیرون از TE(%)، سبب میشه عملکرد آزمایشگاه به طور کاذب پذیرفته بشه؛ یعنی «پذیرش کاذب» (False Acceptable) و یا «منفی کاذب».
البته خیلی وقتها میبینیم که مقادیر TE(%) بیولوژیک، کنار خطاهای مجاز CLIA و RCPA و… به عنوان یکی از منابع TEa برای مدل خطای کل استفاده میشه. اگرچه مقادیر TE(%) در اصل واسه این کار درست نشدن اما استفاده از اونها به این شکل اشکالی نداره. نکته مهم اینه که حواسمون باشه این دو تا رویکرد، یعنی «خطاهای مجاز جداگانه» و «خطای کل»، رو با هم قاطی نکنیم. اشتباهی که توی چند سال اخیر توی ایران دیده میشه؛ در حالی که مراجع نظارتی از آزمایشگاهها میخوان از مدل خطای کل و قوانین پک وستگارد- که برای مدل خطای کل طراحی شده- استفاده بکنن، همزمان از آزمایشگاه میپرسن: «CV مجازت چقدره؟»!
نکته مهم دیگه اینه که اگرچه TE(%) بیولوژیک از ترکیب B(%) و I(%) به دست میآد، اما همونطور که در بالا توضیح داده شده، این که برای منظور خاصی (یعنی استفاده توسط مؤسسات پکخ تو اروپا) انجام شده و هرگز به این معنی نیست که توی مدل خطای کل هم، CV مجاز و Bias مجاز داریم و از ترکیب اونها، TEa حساب میشه. به هیچ عنوان توی توضیحات همراه جدولهای CLIA و RCPA و… خبری از این حرفها نیست. توی هیچ کدوم نه حرفی از CV مجاز و Bias مجاز به صورت جدا هست و نه هیچ فرمولی و راهکاری برای به دست آوردن TEa از CV و Bias به اصطلاح مجاز.
مثلاً نویسندههای جدول RCPA توضیح میدن که هدفشون این بوده که (نقل به مضمون) «مقادیری برای خطای مجاز ارائه بدن که هم نیاز بالین رو در نظر گرفته باشه، هم سطح فعلی فناوری رو و هم امکانات و منابع آزمایشگاهها رو. برای رسیدن به این هدف، افراد صاحبنظر از طرفهای مختلف شامل پزشکها، تولید کنندههای محصولات آزمایشگاهی، آزمایشگاهیها، برنامههای پکخ، نهادهای نظارتی و نمایندههای نهادهای قانونی، دور هم نشستن، بحث و گفتگو کردن و روی مقادیر ارائه شده تو جدول RCPA توافق کردن.»
تأثیر تکرار سنجش بر خطای کل مجاز
مژده: بالاخره بعد از خوندن این توضیح و تفصیل (امیدوارم مربوط)، کم کم داریم میرسیم به نقد «خطای کل مجاز تعدیل شده».
خطای کل مجاز، مثل هر حد مجاز دیگهای، یه خط قرمزه که ما نباید از اون رو رد بشیم و سعی کنیم تا جایی که میشه عملکردمون از اون بهتر باشه تا پایش عملکرد، سادهتر و ارزونتر بشه. مثلاً اگه حداکثر دمای مجاز برای سردخونه نگهداری میوه 10 درجه سلسیوس باشه، معنیش اینه که اگه دمای یه سردخونه بیشتر از 10 درجهس به اون مجوز فعالیت نمیدن چون میوهها توی دمای بالای 10 درجه خراب میشن.
فرض کنیم یه سردخونهدار با دستگاه خنک کنندهش همه زورش رو میزنه و حداقل دمایی که میتونه ایجاد بکنه میشه 14 درجه. دست آخر تصمیم میگیره 2 تا دستگاه بذاره و از قضا تصمیمش جواب میده و 2 تا دستگاه میتونن با هم دما رو به 9 درجه برسونن. بعد هم تصمیم میگیره برای این که دما پائینتر بره تا خیالش از جهت پایش دما راحتتر بشه، 3 تا دستگاه بذاره و اینجوری دما رو میرسونه به 5 درجه.
پرسش اینه که آیا، حالا که به عوض 1 دستگاه خنککننده از 2 تا یا 3 تا دستگاه استفاده میکنه، باز هم دمای مجاز همون 10 درجهس؟ آیا باید دمای مجاز رو برای استفاده از 2 تا دستگاه، کمی پائینتر از 10 درجه در نظر بگیریم و برای 3 تا دستگاه خیلی کمتر؟ آیا باید به اون سردخونهدار مثلاً بگیم با 2 تا دستگاه، دمای مجاز واسه تو میشه 9 درجه و اگه 3 تا دستگاه بذاری دمای مجاز برات میشه 4 درجه؟ البته که نه! دمای یه سردخونه باید زیر 10 درجه باشه تا میوهها سالم باشن.
1 دستگاه بذاره یا 2 تا یا 3 تا یا بیشتر، دمای مجاز همون 10 درجهس، چون توی دمای کمتر از 10 درجه میوهها سالم میمونن؛ فقط همین! اگه به این دلیل که از بیشتر از 1 دستگاه استفاده میشه دمای مجاز رو کمتر از 10 درجه در نظر بگیریم، اون سردخونهدار حق داره اعتراض بکنه که کلی هزینه کرده دمای سردخونهش بره زیر خط قرمز 10 درجه، نه این که ما هم از اون طرف، خط قرمز رو پائینتر بیاریم، و البته حق داره به ما بگه: «شما گفتین اگه دما از 10 درجه کمتر باشه میوهها سالم میمونن. به چه دلیل اگه دما رو با 1 دستگاه به زیر 10 درجه برسونم میوهها سالم میمونن اما اگه با بیشتر از 1 دستگاه این کار رو بکنم میوهها سالم نمیمونن؟ مگه واسه میوهها فرقی داره من با چند تا دستگاه دمای سردخونهم رو میبرم زیر 10 درجه؟»
به عنوان مثالی دیگه، فرض کنیم برای کارمندهای یه بانک، مدت تأخیر مجاز برای ورود به محل کار 20 دقیقه است. التبه که این مرز مجاز، ربطی نداره به این که یه کارمند با چه وسیلهای میره سر کار: پیاده، با دوچرخه، با موتوسیکلت و غیره. به هر شکلی که یه کارمند بره سر کار، مهم اینه که بیشتر از 20 دقیقه تأخیر نداشته باشه. فرض کنیم یه کارمند چند روز پیاده میآد و میبینه تأخیرش بیشتر از 20 دقیقه میشه. واسه همین از روزهای بعد با دوچرخه میآد و از قضا مشکلش برطرف میشه و تأخیرش حدود 14 دقیقه میشه. قطعاً به اون نمیگیم حالا که با دوچرخه میایی، پس تأخیر مجاز برای تو تعدیل میشه و از 20 دقیقه میرسه به 15.
یا اگه بعد از مدتی یه موتوسیکلت خرید که هم خیالش از بابت به موقع رسیدن راحتتر بشه و هم کمی زودتر برسه تا با حوصلهتر کارش رو شروع بکنه، و تأخیرش شد حدود 5 دقیقه؛ صداش نمیکنیم دفتر به اون بگیم «چون با موتوسیکلت میآی تأخیر مجاز برات میشه 7 دقیقه». اگه مرز تأخیر مجاز رو به خاطر استفاده از دوچرخه یا موتوسیکلت کمتر بکنیم (یا به اصطلاح تعدیل بکنیم)، اون کارمند حق داره اعتراض بکنه که برای خرید دوچرخه هزینه کرده و بعد برای خریدن موتوسیکلت هزینه بیشتری کرده که زمان تأخیرش رو کم بکنه نه این که ما هم از اون طرف، تأخیر مجاز رو کمتر بکنیم، و حق داره به ما بگه: «شما گفتین چون اول صبح مشتریها تک و توک هستن اگه تأخیرم کمتر از 20 دقیقه باشه مشکلی پیش نمیآد.
حالا به چه دلیلی اگه با دوچرخه بیام، بعد از 15 دقیقه مشکل پیش میآد و اگه با موتوسیکلت بیام بعد از 7 دقیقه؟ مگه تعداد مشتریهای اول صبح بستگی داره به این که من با چه وسیلهای خودم رو به بانک میرسونم؟»
توی مثالهای بالا و البته در موارد دیگه، مرز خطای مجاز باید ثابت باقی بمونه؛ فارغ از این که افراد به چه صورتی عملکردشون رو اصلاح میکنن تا بتونن معیار خطای مجاز رو برآورده بکنن. ما زحمت بیشتری میکشیم، وقت بیشتری صرف میکنیم و هزینه بیشتری متحمل میشیم که از پس خطای مجاز بر بیائیم؛ نه این که به نسبت زحمت، وقت و هزینه بیشتری که ما متحمل میشیم مرز خطای مجاز هم تعدیل بشه.
البته که فرمولهایی وجود داره برای ارتباط دادن دمای سردخونه با تعداد دستگاه سردکننده و برای ارتباط دادن وسیله رفتن به محل کار با مدت تأخیر؛ اما این فرمولها برای اینه که حساب کنیم در صورت افزایش هزینه و تلاش، عملکرد ما چقدر بهتر میشه وخطای ما چقدر کمتر میشه نه این که از این فرمولها استفاده کنیم واسه کاهش و به اصطلاح تعدیل خطای مجاز.
یه بار دیگه بریم سراغ مثال اندازهگیری طول کوچهها که به اندازهگیری غلظت مواد تو آزمایشگاه نزدیکتره. اول معیارهای شهرداری یادمون بیاد: (الف) اختلاف مجاز = 10%؛ (ب) درصد مجاز برای اندازه نادرست = 5%. این نکته هم یادمون بیاد که چه در مورد متر زدن کوچهها و چه در مورد آزمایش نمونهها توی آزمایشگاه، تمرکزمون روی خطای تکتک جوابها نیست، بلکه تمرکزمون روی اینه که مطمئن بشیم عملکردمون خوبه؛ به این معنی که اختلاف حداقل 95% از جوابهامون کمتر از خطای کل مجازه؛ یا به عبارت دیگه، حداقل 95% از جوابهامون میافته توی محدوده قابل قبول (TV ± TEa).
از منظر یه جواب تکی، اگه طول واقعی یه کوچه 100 متر باشه و ما 108 متر گزارش بکنیم، جوابمون درسته چون اختلافش با مقدار واقعی از 10% کمتره؛ همین و بس! دیگه کاری ندارن ما 1 بار متر زدیم، یا واسه کم کردن CV اندازهگیریمون، چند بار متر زدیم و میانگین گرفتیم. در هر صورت، خطای مجاز واسه اندازهگیری طول کوچهها برابره با 10% و به هیچ عنوان بسته به دفعات سنجش کم یا تعدیل نمیشه. با هر تعداد تکرار که ما نتیجه رو به دست آورده باشیم، اگه اختلافش با مقدار واقعی کمتر از 10% باشه واسه کار شهرداریچیها کافییه و اونها رو توی تصمیمات عمرانیشون گمراه نمیکنه.
اگه این جواب 108 متر حاصل مثلاً میانگین گرفتن از 3 بار اندازهگیری باشه، این دلیلی نمیشه که شهرداری بگه «حالا چون شما 3 بار متر زدی و میانگین گرفتی، پس خطای کل مجاز با فرمول mTEa تعدیل میشه و میشه 7.2%؛ متأسفیم، بر اساس این mTEa، جواب 108 شما نادرسته». اگه شهرداری همچین ادعایی بکنه ما حق داریم بگیم «شما گفتین اگه اختلاف جواب ما با مقدار واقعی کمتر از 10% باشه، شما تو محاسباتتون واسه تصمیمات عمرانی دچار اشتباه نمیشین. حالا به چه دلیلی اگه ما به جای 1 بار، 3 بار متر بزنیم و میانگین بگیریم، اختلاف مجاز باید کمتر از 7.2% باشه تا شما تو تصمیمهاتون دچار اشتباه نشین؟ مگه «حداکثر اختلاف مجاز» واسه اشتباه نکردن شما به دفعات اندازهگیری ما ربط داره؟»
حالا از منظر عملکرد هم که به موضوع تعدیل خطای کل نگاه کنیم. با فرض TEa برابر 10%؛ اگه Bias متر ما 1% و CV اون 6% باشه، خطای سنجشی کل میشه 12% که از TEa بزرگتره و عملکردمون قابل قبول نیست. اگه مترمون رو بدیم برامون کالیبر بکنن و Bias صفر بشه، عملکرد بهتر میشه اما مشکل کاملاً حل نمیشه چون خطای سنجشی کل میشه 11% که هنوز هم از TEa بزرگتره. پس تصمیم میگیریم هر کوچه رو 2 بار متر بزنیم و میانگین بگیریم. با این کار CV ما میشه 4.2% و خطای سنجشی کل هم میشه 8.4%. با این خطای سنجشی کل، بیشتر از 95% از نتایج ما درسته و طبق قراری که با شهرداری داشتیم عملکردمون خوبه.
مطمئناً قبول نمیکنیم که شهرداری بگه «نه، قبول نیست! چون شما 2 بار متر زدین، پس TEa با فرمول mTEa براتون تعدیل میشه و میشه 8%». اگه همچین چیزی بگه ما حق داریم اعتراض کنیم که «چه فرقی میکنه ما 1 بار متر زدیم یا 2 بار یا چند بار؟ مهم اینه که طبق الزامات کیفیت که توی قرارداد نوشته شده، باید حداقل 95% از نتایج ما کمتر از 10% با مقدار واقعی اختلاف داشته باشه که با Bias برابر صفر و CV برابر 4.2% این شرط شما برآورده شده.»
در مورد نتایج آزمایشگاهی هم همین طوره؛ فارغ از این که 1 بار نمونه رو سنجش میکنیم یا چند بار، خطای کل مجاز در هر حالت یکسانه. از منظر یه جواب تک، مهم اینه که اون جواب بیشتر از TEa از مقدار واقعیش دور نباشه تا موجب تصمیمات اشتباه نشه. به عنوان مثال، از مثالی که توی صفحه 57 کتاب طرح شده استفاده میکنم. با فرض TEa برابر 7% برای سنجش کراتینین؛ مقدار هدف (مقدار واقعی) کراتینین تو یه نمونه mg/dL 2.5 بوده و آزمایشگاه mg/dL 2.6 گزارش کرده. آیا جوابش درسته؟ اختلاف جواب آزمایشگاه با مقدار هدف برابره با mg/dL 0.1 که نسبت به مقدار هدف میشه 4% و چون 4% اختلاف از 7% اختلاف مجاز کمتره، این جواب درسته؛ همین!
دیگه کاری نداریم به این که جوابی که آزمایشگاه داده حاصل 1 بار سنجشه یا 2 بار یا 16 بار (تکرارهای مطرح شده در مثال کتاب). در هر حال جواب 2.6 کمتر از 7% با 2.5 اختلاف داره و بنا بر این موجب اشتباه در تصمیمگیریهای بالینی نمیشه. مطمئنا این طور نیست که اگه این جواب 2.6 رو با 1 بار سنجش به دست آورده باشیم، جواب خوبییه، چون 4% اختلاف موجب اشتباه در تصمیمهای بالینی نمیشه؛ اگه با 2 بار سنجش به دست آورده باشیم، بد نیست چون هنوز هم 4% اختلاف سبب اشتباه بالینی نمیشه؛ اما اگه همین 2.6 حاصل 16 بار سنجش باشه به درد نمیخوره چون دیگه 4% اختلاف خیلی زیاده و شدیداً منجر به اشتباهات بالینی میشه.
از قضا سرکه انگبین صفرا فزود! این همه تکرار کردیم که کار بهتر بشه، بدتر شد. اینجاس که آدم سادهای مثل من هاج و واج میپرسه: «یعنی چی؟ مگه حد و مرز 7% واسه این نیست که اگه اختلاف جواب با مقدار واقعی کمتر از این حد باشه، موجب اشتباهات بالینی نمیشه؟ پس چرا 4% اختلاف با 1 بار سنجش خوبه، با 2 بار سنجش بدک نیست و با 16 بار سنجش خیلی بده؟» چون mTEa واسه 2 تکرار شده 5.6% و برای 16 بار تکرار شده 3.5%؟ خوب موضوع اینه که اساساً نباید همچین محاسبهای انجام بشه.
به همین دلیل، یعنی این که هر جور که آزمایشگاه جواب رو به دست بیاره در هر حال خطای مجاز ثابته و نباید بسته به دفعات تکرار آزمایش تعدیل بشه، برنامههای پایش کیفیت خارجی مثل CLIA، CAP، RiliBak، UK-NEQAS (بریتانیا) و SKLM (هلند) که برنامههای «درستی-بنیان» (Accuracy-Based) هستن و نتایج آزمایشگاه رو با مقدار واقعی حاصل از روشهای مرجع مقایسه میکنن، از آزمایشگاهها نمیپرسن چند بار نمونهها رو سنجش میکنن تا خطای مجاز رو براشون تعدیل بکنن. در حالی که به آزمایشگاهها گوشزد میکنن و تأکید میکنن که فقط در صورتی اجازه دارن نمونه کنترل رو 2 بار یا 3 بار یا بیشتر سنجش بکنن و میانگین بگیرن که این کار رو به طور معمول برای نمونههای بیمارها هم انجام میدن، اما هرگز ادامه نمیدن که مثلاً «در صورت تکرار سنجش، تعداد دفعات تکرار رو گزارش بکنین که خطای مجاز برای آزمایشگاه شما تعدیل بشه».
تو مثال بالا از منظر درستی/نادرستی یه تک-جواب به موضوع نگاه کردیم؛ اما همونطور که پیشتر تکرار شد، توی «مدل خطای کل» روی درستی/نادرستی عملکرد تمرکز میشه نه تک-جوابها. به عنوان مثال، اگه یه روش سنجش گلوکز داشته باشیم با Bias برابر 2% و CV برابر 6.5%، خطای سنجشی کل میشه 15% که با معیار CLIA از TEa برابر با 10% بزرگتره و این عملکرد قابل قبول نیست. برای بهبود عملکرد، دستگاه رو خوب کالیبر میکنیم و Bias رو کاملاً حذف میکنیم و در نتیجه TAE میشه 13% که هنوز هم از TEa بزرگتره. بنا بر این، تصمیم میگیریم نمونهها رو 3 بار تکرار کنیم و میانگین بگیریم. با این ترفند، CV از 6.5% به 3.8% کم میشه و در نتیجه TAE ما میشه 7.6%. حالا میتونیم بیشتر از 95% جواب درست تولید بکنیم و عملکردمون قابل قبوله.
خلاصه این که با تحمل زحمت و هزینه 3 بار سنجش موفق شدیم از پس تولید حداقل 95% جواب درست بربیائیم. حالا هیچ دلیلی نداره به ما بگن «چون 3 بار سنجش میکنین، TEa واسه شما تعدیل میشه و میشه 7.2% و چون خطای کل شما شده 7.6% پس عملکرد شما قابل قبول نیست». معلومه که اعتراض میکنیم و میگیم «شما گفتین اگه حداقل 95% جوابهامون درست باشه عملکرد ما خوبه، چون پزشک میتونه نسبت به هر جواب گلوکزی که ما گزارش میکنیم حداقل 95% مطمئن باشه که اون جواب درسته. خطای کل ما نشون میده که ما بیشتر از 95% جواب درست تولید میکنیم؛ به چه دلیل اگه 1 بار سنجش کار میکردیم، پزشک میتونست حداقل 95% به درستی جوابهای ما اطمینان بکنه، اما حالا که با 3 بار سنجش (یا هر چند بار دیگه) کار میکنیم پزشک نمیتونه حداقل 95% به درستی جوابها اطمینان بکنه؟»
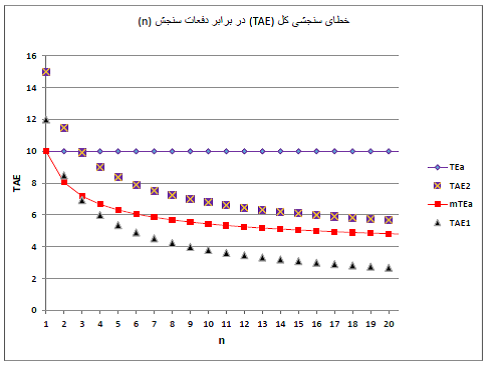
شکل زیر چکیده بحث بالا رو نشون میده. از دو روش 1 و 2 برای آزمایشی با خطای کل مجاز 10% استفاده شده. CV هر دو روش برابره با 6%، عدم صحت روش شماره 1 صفره، اما عدم صحت روش شماره برابره با 3%. با این دادهها، خطای سنجشی کل به ترتیب میشه 12% و 15%؛ که برای هر دو روش غیر قابل قبوله. خسک برای روش اول فقط با 2 تکرار میرسه به حد مجاز 10% اما برای روش دوم، 3 تکرار لازمه تا به 10% برسه.
با تکرارهای بیشتر، خسک هر دو روش به سرعت از 10% کمتر میشه؛ یعنی با ثابت در نظر گرفتن خطای کل مجاز (لوزی- خط بنفش تو شکل زیر)، افزایش تکرار سبب میشه TAE به اندازه کافی از TEa کمتر بشه و فضای بیشتری برای پک باقی بمونه. فضای بیشتر برای پک، به این معنییه که میتونیم کیفیت کارمون رو با معیارهای سادهتر و با هزینه و زحمت کمتری پایش بکنیم.
اما اگه قرار باشه به دلیل تکرار سنجش، خطای کل مجاز رو هم با فرمول mTEa کم بکنیم و از mTEa برای قضاوت در باره کیفیت سنجش استفاده بکنیم (مربع-خط قرمز)، TAE روش دوم حتا با 20 تکرار هم از mTEa بالاتر میمونه و بنا بر این کیفیت اون غیر قابل قبول به حساب میآد. TAE روش اول با 3 تکرار میره زیر mTEa اما حتا تا 20 تکرار هم فاصله چندانی از mTEa نمیگیره و فضای چندانی برای پک ایجاد نمیشه. نداشتن فضای کافی برای پک به این معنییه که برای پایش کیفیت باید از معیارهای چند-قانونی سخت استفاده کرد و هزینه و زحمت بیشتری رو متحمل شد.
این موضوع که خطای مجاز ثابته و بسته به عملکرد آزمایشگاه تعدیل نمیشه فقط مختص مدل خطای کل نیست، بلکه توی جاهایی هم که به عوض خطای کل مجاز، از CV مجاز و Bias مجاز به طور جداگانه استفاده میشه موضوع همینطوره. I(%) و B(%) (CV مجاز و Bias مجاز) رو به آزمایشگاهها اعلام میکنن و میگن حواستون باشه CV و Bias روش شما از این مقادیر مجاز بیشتر نشه؛ فقط همین! دیگه کاری ندارن شما با چه ترفندی CV و Bias رو میبرید زیر مزر مجاز تا به اصطلاح مرز مجاز رو براتون تعدیل بکنن.
یه کم توضیح در باره نوسان بیولوژیک. به نظر میآد توی وضعیت سلامتی، غلظت مواد داخل مایعات بیولوژیک مثل خون و ادرار و غیره، اطراف یه «نقطه تنظیم» (Set-point) نوسان میکنه. به این نوسان میگیم «CV درون- فردی» (Intra-individual CV; CVI). علاوه بر این، نقطه تنظیم همه افراد سالم یکسان نیست و افراد مختلف، نقطه- تنظیمهای مختلف دارن. به پراکندگی نقطه- تنظیمها بین افراد میگیم «CV گروه» (Group CV; CVG). برای تعیین CVهای بیولوژیک، بسته به ماده مورد نظر، از تعدادی آدم سالم چند بار در زمانهای مختلف نمونه میگیرن و میانگین و CV هر فرد رو تعیین میکنن. از CVهای افراد، میانگین میگیرن که میشه CVI و از میانگینهای افراد (که نماینده نقطه- تنظیمهای افراده)، CV میگیرن که میشه CVG.
استدلال پشت CV مجاز بیولوژیک، اینه که وقتی برای پیگیری تغییر در وضعیت یه بیمار، دو تا جواب متوالی رو با هم مقایسه میکنیم، CV آزمایشگاه باید اینقدر بزرگ نباشه که نتونیم با اطمینان، تفاوت دو تا نتیجه رو بذاریم به حساب تغییر در وضعیت بیمار و شک کنیم «نکنه این اختلاف بین دو تا نتیجه به خاطر بزرگ بودن CV آزمایشگاه باشه». پراکندگی نتایج متوالی یه بیمار، در حالی که وضعیت بیمار پایداره و نقطه- تنظیم ثابته، ناشی میشه از CV درون-فردی (CVI) و CV سنجش. با این استدلال، پیشنهاد کردن برای این که CV سنجش خیلی به پراکندگی نتایج اضافه نکنه، مقدار CV سنجش حداکثر نصف CV درون- فردی باشه:
I(%) = 0.5 * CVI
I(%) رو به آزمایشگاهها اعلام میکنن و میگن CVتون از این بیشتر نباشه؛ فقط همین. هیچ وقت به آزمایشگاهها مثلاً نمیگن «این CVهای مجاز واسه وقتییه که نمونهها رو 1 بار آزمایش میکنین؛ اگه بیشتر از 1 بار سنجش کردین و میانگین گرفتین، باید CV مجاز رو در 1/√n ضرب بکنین تا تعدیل بشه».
مثلاً اگه I(%) برای یه آزمایش 3% باشه معنیش اینه که تا وقتی که CV آزمایشگاه کمتر از 3% باشه میشه با اطمینان جوابهای متوالی بیمار رو با هم مقایسه کرد. حالا اگه CV یه آزمایشگاه بیشتر از 5% بود و اون آزمایشگاه همه تلاشش رو کرد (شامل تعمیر دستگاه، حذف نوسانات برق، آموزش کاربر،…) و نتونست CV رو از 4% کمتر بکنه، ممکنه به عنوان یکی از آخرین ترفندها تصمیم بگیره نمونهها رو بیشتر از 1 بار سنجش بکنه تا CVش از 4% هم کمتر بشه بره زیر 3%. مثلاً اگه نمونهها رو 2 بار سنجش بکنه، CVش از 4% میشه 2.8% و قابل قبول میشه. اگه CV یه آزمایشگاه دیگه 5% باشه و راه دیگهای غیر از سنجش تکراری واسه کم کردن CV نداشته باشه، باید نمونهها رو حداقل 3 بار تکرار بکنه تا CV بشه 2.9% و قابل قبول بشه.
کاملاً معلومه که فارغ از این که CV آزمایشگاه به چه شکلی کمتر از CV مجاز شده، بدون تکرار، 2 بار تکرار، 3 بار تکرار، یا بیشتر، در هر حال تا وقتی که آزمایشگاه بتونه با CV کمتر از 3% کار بکنه میشه با اطمینان نتایج متوالی بیمار رو با هم مقایسه کرد. اگه بنا باشه آزمایشگاه با سنجش تکراری نمونهها، زحمت و هزینه بیشتری رو متحمل بشه که CV رو پایین بیاره، اما بعد به اون بگیم «خوب، حالا باید I(%) رو هم بسته به دفعات تکرار با استفاده از ضریب 1/√n تعدیل بکنی»، عملاً زحمت آزمایشگاه رو دود کردیم.
اگه در مورد مثالهای بالا این کار رو بکنیم؛ با 2 بار تکرار، CV آزمایشگاه از 4% میشه 2.8% اما I(%) هم کم میشه و به عوض 3% میشه 2.1%؛ و با 3 بار تکرار، CV آزمایشگاه از 5% میشه 2.3% اما I(%) هم تعدیل میشه و به عوض 3% میشه 1.7%. اگه همچین تعدیلی رو پیشنهاد بکنیم، آزمایشگاه حق داره بگه «شما گفتین اگه CV زیر 3% باشه مشکلی واسه مقایسه نتایج متوالی بیمار پیش نمیآد.
من هم از راه تکرار سنجش، CV رو بردم زیر 3%؛ به چه دلیل اگه با 1 بار سنجش جواب میدادم، CV کمتر از 3% واسه مقایسه نتایج متوالی خوب بود اما با جواب حاصل از بیشتر از 1 بار سنجش، CV کمتر از 3% دیگه کافی نیست و باید CV مجاز تعدیل بشه؟ آخه CV مجاز که اون طرف داستان بر اساس نیاز بالین تعیین شده و ربطی به دفعات تکرار من نداره».
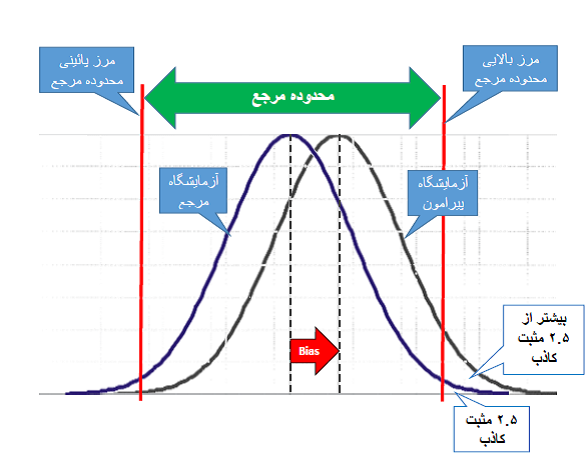
استدلال پشت تعیین Bias مجاز بیولوژیک، اینه که آزمایشگاهها هر کدوم به صورت فردی واسه آزمایشها «محدوده مرجع» (Reference Range) (به اصطلاح رایج «رنج نرمال») تعیین نکنن، بلکه یه «آزمایشگاه مرجع» با استفاده از روش مرجع، این کار رو بکنه و بقیه آزمایشگاهها (به اصطلاح «آزمایشگاههای پیرامون») اون محدوده مرجع رو تو گزارش جوابهاشون استفاده بکنن. موقع تعیین محدوده مرجع، بعد از نمونهگیری از یه تعداد آدم سالم (افراد مرجع)، اندازهگیری نمونهها و تعیین نتایج؛ از نتایج میانگین و انحراف معیار میگیرن و بازهای رو که 95% از نتایج میانی توی اون قرار داره، به عنوان محدوده مرجع گزارش میکنن.
با این حساب، محدودههای مرجع طوری تعیین میشن که در هر طرف، 2.5% از نتایج آدمهای سالم میافته بیرون و به اصطلاح از هر طرف 2.5% «مثبت کاذب» داریم. اگه روش آزمایشگاه پیرامون نسبت به روش آزمایشگاه مرجع Bias داشته باشه، اون وقت توی طرفی که Bias هست بیشتر از 2.5% مثبت کاذب ایجاد میشه؛ هر چی Bias بزرگتر، مثبت کاذب تو طرف Bias بیشتر (شکل زیر).
پیشنهاد شده Bias آزمایشگاه پیرامون حداکثر اینقدر باشه که درصد مثبت کاذب توی طرف Bias از 4.6% بزرگتر نشه. چون پراکندگی نتایجی که آزمایشگاه مرجع از نمونههای افراد مرجع به دست میاره به منابع نوسان بیولوژیک، یعنی CVI و CVG، بستگی داره، Bias مجاز B(%) رو از روی CVI و CVG تعیین کردن:
B(%) = 0.25 x ( CVI2 + CVG2)0.5
در مورد B(%) هم فقط به آزمایشگاهها میگن حواستون باشه عدم صحتتون از این بیشتر نشه و دیگه کاری ندارن آزمایشگاه با چه ترفندی عدم صحتش رو میبره زیر درصد مجاز تا بر اساس اون B(%) رو تعدیل بکنن. به هر شکلی که آزمایشگاه بتونه Bias رو برسونه زیر B(%)، پزشکها میتونن با خیال راحت نتایج اون آزمایشگاه رو با محدودهها مرجعی که از طرف یه مرکز مرجع تعیین شده مقایسه بکنن بدون این که تصمیمهای بالینی اشتباه واسه بیمارهاشون بگیرن.
نقش تکرار سنجش در عدم قطعیت
باز هم بدون وارد شدن تو جزئیات؛ عدم قطعیت اندازهگیری (Measurement Uncertainty, MU) بازهای رو تعیین میکنه که با یه احتمال معین، مقدار واقعی توی اون بازه قرار میگیره. مثلاً اندازه یه کوچه 200 متر با عدم قطعیت 95% برابر 2% گزارش شده، این یعنی به احتمال 95% طول واقعی کوچه یه مقدارییه بین 2%±200 متر (196 تا 204 متر) و فقط 5% احتمال داره که طول واقعی کوچه کمتر از 196 متر یا بیشتر از 204 متر باشه. حالا اگه یه مهندس عمران بخواد مصالح و هزینههای لازم واسه سنگفرش کردن اون کوچه رو حساب بکنه، نباید حساب کتابش برای دقیقاً 200 متر باشه، بلکه باید عدم قطعیت اندازهگیری رو هم در نظر بگیره. هر چی عدم قطعیت اندازهگیریها کوچیکتر باشه، خیال کاربری که از نتایج استفاده میکنه راحتتره و با اطمینان بیشتری تصمیمگیری میکنه.
بر عکس، هر چی عدم قطعیت بزرگتر باشه، اطمینان به نتایج کمتر میشه و با شک و تردید بیشتری از اون نتایج استفاده میشه؛ مثلاً اگه توی این مثال گفته بودن عدم قطعیت با احتمال 95% برابره با 20%، اون وقت اون مهندس عمران باید در نظر میگرفت که با احتمال 95% طول واقعی کوچه بین 160 متر و 240 متره (و البته 5% هم احتمال داره که از 160 متر کمتر یا از 240 متر بیشتر باشه). حالا اگه بخواد واسه سنگفرش اون کوچه حساب کتاب بکنه، باید به قول عمرانیها «تولرانس» زیادی رو در نظر بگیره؛ شاید اینقدر زیاد که از تولرانس مهندس بیشتر بشه و از خیر جوابهای اون شرکت اندازهگیری/ آزمایشگاه بگذره و کوچه/ مریض رو بفرسته یه شرکت/ آزمایشگاه دیگه (به طور کلی، یه «اندازهگیریکده» دیگه).
داستان عدم قطعیت توی آزمایشگاه هم همینطوره. اگه یه جواب گلوکز رو mg/dL 110 گزارش بکنیم با عدم قطعیت 20% با احتمال 95%، این گزارش میگه غلظت واقعی گلوکز به احتمال 95% یه مقدارییه بین 88 تا 132؛ یعنی جواب واقعی ممکنه توی محدوده طبیعی باشه (کمتر از 100)، توی محدوده بینابینی باشه (100 تا 125)، یا توی محدوده دیابتی باشه (بیشتر از 125). اگه این رو به یه پزشک بگیم، مسلماً نمیتونه با خیال راحت در باره بیمار تصمیم بگیره؛ چه تشخیصی بذاره: گلوکز این بیمار طبیعییه؟ بینابینییه؟ یا بیمار دیابت داره؟ اما اگه عدم قطعیت برابر 2% باشه، غلظت واقعی گلوکز به احتمال 95% یه مقدارییه بین 108 تا 112 و پزشک با خیال خیلی راحتتری تصمیمگیری بالینی میکنه.
حتا اگه پزشک بیشتر از 95% اطمینان بخواد، عدم قطعیت برای احتمال 99.7% برابره با 3% و این یعنی 99.7% مطمئن باش که غلظت واقعی گلوکز یه مقداریه بین 107 تا 113 و فقط 0.3% احتمال داره که مقدار واقعی کمتر از 107 یا بیشتر از 113 باشه.
عدم قطعیت سنجشهای آزمایشگاهی به سه عامل بستگی داره: انحراف معیار سنجش (SD)، عدم قطعیت کالیبراتور (ucal) و عدم قطعیت Bias (uBias)؛
u = √(SD2 + ucal2 + uBias2)
به این u میگیم عدم قطعیت معیار (Standard Uncertainty) (یه نکته کوچیک: به u میگیم عدم قطعیت معیار چون در واقع «انحراف معیار» کلی حاصل از این سه تا عامله). اگه نتیجه رو با R نشون میدیم، با داشتن u میتونیم بگیم که مقدار واقعی با اطمینان 68% یه جایییه تو بازه R ± u (یه یادآوری کوچیک: توی توزیع گوسی، 68% از سطح وسط منحنی میافته تو فاصله X̄ ± 1SD). چون اطمینان 68% نسبتاً کمه، u رو دو برابر میکنیم، به اون میگیم «عدم قطعیت بسط یافته» (Expanded Uncertainty) و با نشانه U نشون میدیم. با داشتن U، میتونیم بگیم مقدار واقعی با اطمینان 95% یه جاییه توی فاصله R ± U. اگه اجزای طرف راست فرمول u رو به صورت درصدی از نتیجه بنویسیم، عدم قطعیت به صورت درصد ، u%، حساب میشه:
%u= √(CV2 + %ucal2 + %uBias2)
%U = 2 x %u
هر کدوم از سه عامل مؤثر در عدم قطعیت که بزرگ باشه، عدم قطعیت نتایج ما بزرگ میشه و جواب ما رو غیر قابل اطمینان میکنه. اگه به خاطر CV بالای سنجش، عدم قطعیت ما بزرگ باشه و کار تصمیمگیری بالینی رو خراب بکنه، یه راه چاره اینه که با سنجش تکراری نمونهها، CV رو کم بکنیم و در نتیجه عدم قطعیت کوچکتری داشته باشیم. به عنوان مثالی از تأثیر تکرار سنجش روی کاهش عدم قطعیت، از همون مثال ذکر شده تو صفحه 57 کتاب استفاده میکنم: یه جواب کراتینین داریم برابر mg/dL 2.6 که حاصل از سه وضعیت مختلفه: 1 بار سنجش، 2 بار سنجش و 16 بار سنجش.
فرض میکنیم CV این روش برابره با 10%، %ucal برابره با 1% و %uBias هم برابره با 1%. عدم قطعیت بسط یافته (U) برای این سه وضعیت به ترتیب میشه: 20.2%، 14.5% و 5.7%. همونطور که میبینیم وقتی برای به دست آوردن جواب، نمونه رو 16 بار اندازه تکرار میکنیم، عدم قطعیت ما به مقدار زیادی کم میشه (که البته انتظار هم همینه) و بنا بر این اطمینانپذیری جواب خیلی بالا میره. با این عدم قطعیتها، در مورد این که غلظت واقعی کراتینین چقدره، میشه با اطمینان 95% گفت:
- اگه نتیجه 2.6 حاصل 1 بار سنجش باشه، غلظت واقعی یه مقدارییه بین 2.1 تا 3.1؛
- اگه نتیجه 2.6 حاصل 2 بار سنجش باشه، غلظت واقعی یه مقدارییه بین 2.2 تا 3.0؛ و
- اگه نتیجه 2.6 حاصل 16 بار سنجش باشه، غلظت واقعی یه مقدارییه بین 2.5 تا 2.7.
همونطور که میبینیم با 1 بار سنجش، جواب واقعی با اطمینان 95% ممکنه تا mg/dL 0.5 دورتر از جواب ما باشه. با 2 بار سنجش هم وضعیت خیلی بهتر نمیشه و جواب واقعی با اطمینان 95% ممکنه تا mg/dL 0.4 دورتر از جواب ما باشه؛ اما با 16 بار تکرار، شرایط خیلی فرق میکنه و جواب واقعی با اطمینان 95% ممکنه فقط mg/dL 0.1 دورتر از جواب ما باشه. اگه ما این اطلاعات رو به یه پزشک بگیم و از اون بپرسیم در کدوم حالت به جواب ما بیشتر اطمینان میکنه و با خیال راحتتری برای بیمارش تصمیم میگیره، مسلماً وضعیت سوم رو ترجیح میده (حتا ممکنه از اون به بعد تو درخواستهاش بنویسه «کراتینین با 16 بار تکرار»!).
حالا پرسش اینه که چطور میشه گفت جواب حاصل از 1 بار سنجش خوبه (چون TAE اون به اندازه کافی از TEa کوچیکتره)، جواب حاصل از 2 بار سنجش هم هنوز خوبه اما نه به اندازه جواب حاصل از 1 بار سنجش (چون TAE اون خیلی از mTEa کوچیکتر نیست)، اما جواب حاصل از 16 بار سنجش اصلاً خوب نیست (چون TAE اون از mTEa بزرگتره)؟! هم همچین ادعایی نادرسته، هم هر جور فرمولی که درست بشه تا همچین چیزی رو نشون بدیم. بدون نیاز به هیچ فرمول و محاسبهای، میشه فهمید که هر چی تکرار اندازهگیری بیشتر بشه کیفیت جواب بهتر میشه، نه بدتر.
برای برآورد کردن میانگین وزن یه جمعیت 10000 نفری، کافی نیست که فقط 1 نفر رو وزن کنیم و وزن اون رو به عنوان برآوردی از میانگین وزن جمعیت در نظر بگیریم. میانگین یه نمونه 2 نفری برآورد بهتریه و البته میانگین یه نمونه 16 نفری برآورد خیلی بهترییه. هر چی CV وزن جمعیت بزرگتر باشه، باید نمونه بزرگتری داشته باشیم برای این که برآورد مطمئنی از میانگین وزن جمعیت داشته باشیم. در مورد سنجشهای آزمایشگاهی هم همینطوره؛ هر چی CV سنجش بزرگتر باشه، تکرار سنجش باید بیشتر بشه تا برآورد مطمئنی از مقدار واقعی داشته باشیم. اگه یه فرمول درست کنیم که با اون نشون بدیم وزن 1 نفر برآورد بهتریه برای میانگین جمعیت تا میانگین وزن 10 نفر و حتا این که میانگین وزن 16 نفر (یا بیشتر) برآورد غیرقابل قبولییه، باید در اون فرمول که مخالف بدیهیاته تجدیدنظر بکنیم.
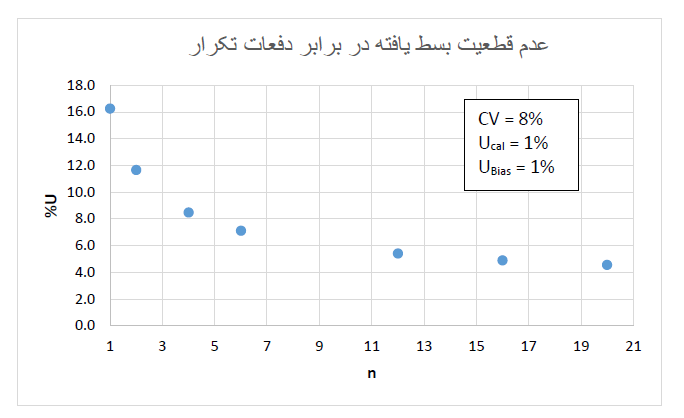
شکل زیر، کاهش عدم قطعیت برای یک روش با CV برابر 8%، %ucal برابر 1% و %uBias برابر 1% رو در برابر افزایش تکرار نشون میده.
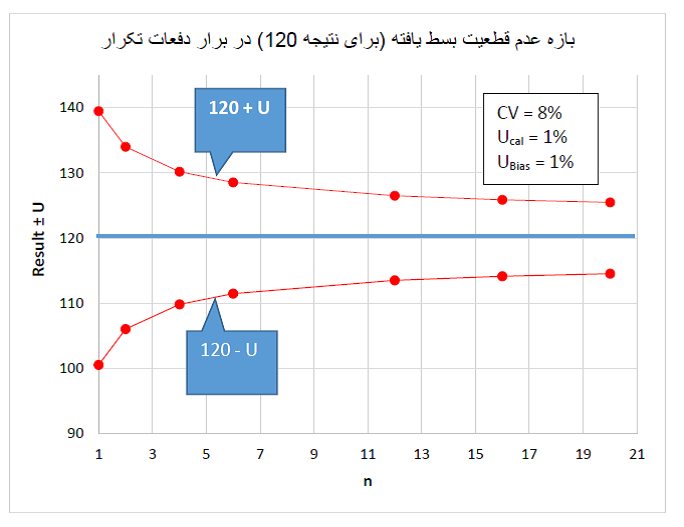
تو شکل بعدی، عدم قطعیتهای شکل بالا برای محاسبه بازه عدم قطعیت 95% برای یه جواب گلوکز برابر با mg/dL 120 استفاده شده. همونطور که دیده میشه با افزایش n، بازه عدم قطعیت باریکتر میشه.
این که با تکرار اندازهگیری جواب مطمئنتری به دست میاریم، موضوعی نیست که به بلد بودن ریاضی و آمار و عدم قطعیت نیاز داشته باشه. افرادی هم که سر و کارشون با این جور مباحث نیست از تکرار اندازهگیری برای اطمینان بیشتر استفاده میکنن. خیلی وقتها شاهد صحنههایی مثل این بودیم که مثلاً یه نجار از شاگردش خواسته طول یه تخته رو اندازه بگیره. وقتی که شاگرد اندازه تخته رو گفته، نجار پرسیده «مطمئنی؟» و شاگرد گفته «آره، 2 بار اندازه گرفتم». وقتی با 2 بار اندازه گرفتن خیال یه نجار راحت میشه، با بیشتر اندازه گرفتن خیالش خیلی راحتتر میشه؛ نه این که بگه «اندازهت قابل قبول نیست چون 10 بار اندازه گرفتی. اگه 1 بار اندازه زده بودی، جوابت مطمئنتر بود».
تکرار سنجش و نوسان بیولوژیک درون-فردی (CVI)
وقتی قراره دو تا جواب پشت سر هم رو با هم مقایسه بکنیم، فقط بزرگ بودن CV سنجش نیست که مشکلساز میشه، بلکه اگه CVI (CV بیولوژیک درون- فردی) هم بزرگ باشه، مشکل ایجاد میکنه. با اقدامات اصلاحی مختلف میشه CV سنجش رو کم کرد، مثل نصب پایدارساز واسه کاهش نوسان برق، نو کردن قطعات کهنه مثل سرنگهای مکنده، …، و دست آخر سنجش تکراری نمونهها. شاید هم کلاً بیخیال اون دستگاه/ کیت بشیم و اون رو با دستگاه/ کیت بهتری جایگزین بکنیم. اما در مورد CVI راه چاره چندانی نداریم؛ مثلاً امکانش نیست که واسه بیمار پایدارساز بذاریم یا روی بیمار کار اصلاحی/ تعمیری روی بیمار انجام بدیم؛ همینطور نمیشه (مثل عوض کردن دستگاه/ کیت) به بیمار بگیم اصلاً بیخیال اون آزمایش بشه و به جای اون یه آزمایش با CVI کوچیکتر براش انجام بدیم.
تنها راه چارهای که برای مشکل بزرگ بودن CVI داریم «تکرار» کردنه. باید بیمار بیشتر از 1 بار و با فاصله زمانی آزمایش بده و پزشک بر اساس میانگین نتایج تصمیم بگیره. به همین دلیله که مثلاً در مورد آزمایش چربیها، برای این که جواب آزمایش برآورد خوبی از نقطه- تنظیم باشه توصیه میشه بیمار طی 1 ماه، 2 بار یا 3 بار آزمایش بده و میانگین نتایج، ملاک تصمیمگیری پزشک باشه. مثلاً با در نظر گرفتن CVI برابر 6% و CV سنجشی برابر 2% برای کلسترول، اگه از بیمار فقط 1 بار نمونه بگیریم و نتیجه بشه mg/dL 220، نقطه- تنظیم کلسترول بیمار با احتمال 95% یه جایییه بین 194 و 246 (فاصله 12% اطراف میانگین) و اگه 2 بار نمونه بگیریم و میانگین نتایج بشه 220، نقطه- تنظیم کلسترول به احتمال 95% یه جایییه بین 202 و 238 (فاصله 8% اطراف میانگین).
اگه دفعات نمونهگیری از 2 بار هم بیشتر بشه، بازهای که نقطه- تنظیم داخلش قرار میگیره باریکتر میشه؛ مثلاً اگه 16 بار از بیمار نمونه بگیریم و از نتایج میانگین بگیریم، نقطه- تنظیم این بیمار با احتمال 95% یه جایییه بین 213 و 227 (فاصله 3% پیرامون میانگین). همونطور که میبینیم، هر چی دفعات تکرار نمونهگیری رو بیشتر میکنیم (مثل تکرار سنجش یه نمونه)، بیشتر میتونیم به نتایج اطمینان بکنیم و این یعنی کیفیت جواب بهتر میشه، نه بدتر. مطمئناً در این مورد هم نمیشه بگیم هر چی دفعات نمونهگیری بیشتر بشه، کیفیت جواب پائینتر میآد چون خطای مجاز تعدیل شدهش کوچکتر میشه.
تأثیر تکرار سنجش بر عیار سیگما و پایش کیفیت
همونطور که میدونیم عیار سیگما (Sigma Metric; SM) کیفیت تولید رو نشون میده و از فرمول زیر حساب میشه:
SM = (TEa – |B|)/SD
یا
SM = (%TEa – |%B|)/CV
هر چی عیار سیگما بالاتر باشه، درصد محصول ناقص کمتره؛ در مورد آزمایشگاه، هر چی عیار سیگما بزرگترباشه، جوابهای نادرست ما کمتره. مثلاً با عیار سیگمای 2، حدود 5% از جوابهای ما میافته بیرون از محدوده مجاز، (نکته: عیار سیگما هم، مثل خطای سنجشی کل، روی کیفیت »عملکرد« تمرکز داره، نه روی کیفیت تک-جواب ها. در واقع، عیار سیگما با دادن اطلاعات در باره نسبت نتایج نادرست، معیاری فراهم میکنه که بدونیم به درست بودن هر تک-جواب چقدر میشه اطمینان داشت). اما با عیار سیگمای 6 فقط 2 تا از 1 میلیارد جواب میافته بیرون از محدوده مجاز. همونطور که توی فرمول عیار سیگما میبینیم، CV تو مخرج فرموله و بنا بر این، برای یه TEa و Bias معین، هر چی CV کوچیکتر بشه به همون نسبت عیار سیگما بزرگتر میشه.
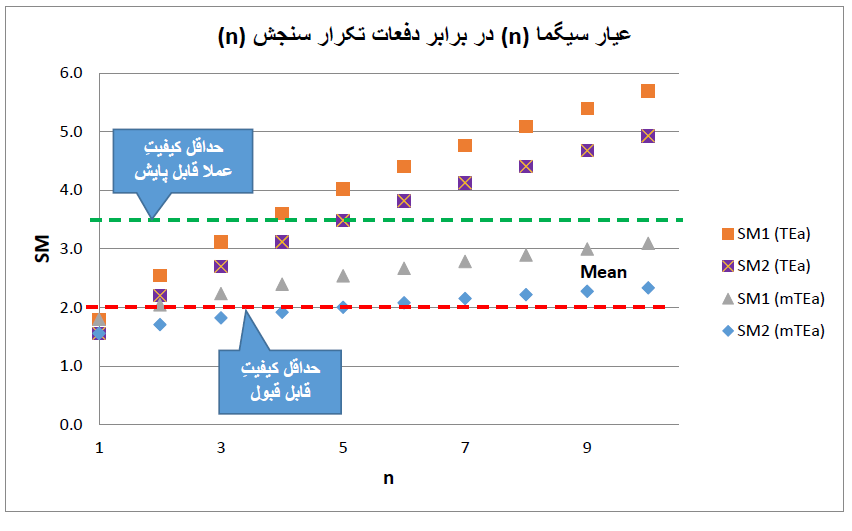
بنا بر این، اگه عیار سیگمامون کوچیک باشه، به عنوان یه گزینه میشه نمونهها رو به صورت تکراری آزمایش کرد تا CV کوچیکتر بشه و به تبع اون SM بزرگتر بشه. شکل زیر عیار سیگمای دو تا روش سنجش مختلف رو برای آنالیتی با TEa برابر 9% نشون میده. CV هر دو روش برابره با 5%، Bias روش شماره 1 صفره اما Bias روش شماره 2 برابره با 3%. با این مشخصات، عیار سیگمای این دو روش به ترتیب برابره با 1.8 سیگما و 1.6 سیگما. همونطور که دو تا نمودار بالایی توی شکل زیر نشون میده، اگه نمونهها به صورت تکراری آزمایش بشه، با زیاد شدن n، عیار سیگما با ثابت گرفتن TEa به طور قابل ملاحظهای بزرگتر میشه.
مثلاً عیار سیگمای روش اول [SM1 (TEa)] با 5 تکرار میرسه به 4 سیگما و با 10 تکرار میرسه به نزدیک 6 سیگما. عیار سیگمای روش دوم [SM2 (TEa)] با 5 تکرار میرسه به 3.5 سیگما و با 10 تکرار میرسه تقریباً به 5 سیگما. در مقابل، اگه بنا باشه به دلیل تکرار، خطای کل مجاز رو تعدیل بکنیم و mTEa رو بذاریم توی فرمول عیار سیگما، زیاد کردن تکرار نمونهها تأثیر چندانی روی بالا رفتن عیار سیگما نمیذاره. مثلاً عیار سیگمای روش اول [SM1 (mTEa)] با 5 تکرار میرسه به 2.5 سیگما و با 10 تکرار میرسه به 3.5 سیگما؛ عیار سیگمای روش دوم [SM2 (mTEa)] با همین تعداد تکرار به ترتیب میرسه به 2 سیگما و 2.3 سیگما.
یادمون بیاد که کمترین عیار سیگمای قابل قبول برابره با 2 سیگما (چون با 2 سیگما، 5% از جوابهای ما نادرسته؛ اگه عیار سیگما از 2 کمتر بشه، درصد جوابهای نادرست ما از 5% بیشتر میشه). همینطور یادمون بیاد که هر چی عیار سیگما بزرگتر باشه، پایش کیفیت راحتتر میشه. مثلاً برای پک یه روش 6 سیگما کافییه فقط یه کنترل تو هر دور بذاریم، از معیار ساده 1:3s استفاده بکنیم و (بر اساس مدل MaxE (Nuf)) برای اطمینان از این که از وقتی که مشکلی پیش میآد تا وقتی که برنامه پک اون رو شناسایی میکنه حداکثر 1 جواب اشتباه اضافی گزارش شده باشه، میتونیم به ازای هر 380 تا نمونه بیمار 1 نمونه کنترل بذاریم (یعنی بعد از خوندن هر 380 تا نمونه بیمار، یه بار هم نمونه کنترل رو بخونیم).
برای پک یه روش 5 سیگما، میشه از همون 1 کنترل و 1:3s استفاده کرد اما باید بعد از هر 50 تا نمونه بیمار یه بار کنترل رو خوند، یا این که 2 تا کنترل تو هر دور بذاریم، معیارمون همون 1:3s باشه و به ازای هر 280 تا نمونه بیمار یه بار کنترلها رو بخونیم. در مقابل، برای پک یه روش 3.5 سیگما، باید 4 کنترل تو هر دور بذاریم (خوندن 2 سطح کنترل 2بار)، معیار چند-قانونی و پرزحمت 1:3s/2of3:2s/R:4s/4:1s رو به کار ببریم و به ازای هر 40 تا نمونه بیمار 2 تا کنترل رو 2 بار بخونیم (یعنی حدود 10% از کار دستگاه و معرفهای ما واسه خوندن کنترلها مصرف بشه).
پایش کیفیت یه روش 3 سیگما از این هم پرهزینهتره: با همون 4 تا کنترل و همون معیار چند-قانونی، باید به ازای هر 11 نمونه بیمار هر 2 کنترل رو 2 بار بخونیم (یعنی تقریباً 30% از هزینه و زحمت ما صرف کنترل خوندن میشه).
به خاطر همینه که اگرچه روشهای با عیار سیگمای 2 تا 3.5 سیگما «قابل قبول» به حساب میان، اما عملاً «غیر قابل کنترل» به حساب میان چون پک اونها عملی و مقرون به صرفه نیست و اگه از اونها استفاده کنیم باید امیدوار باشیم که اشکالی براشون پیش نیاد (ایشالا گربهس!) چون با برنامههای معمول پک، اون اشکالات به سرعت شناسایی نمیشن. با این اوصاف، در مورد روش 1 و 2 در مثال بالا، در صورت به کار بستن تعدیل خطای کل مجاز، حتا 10 بار تکرار هم کمکی نمیکنه چون کیفیت روش شماره 1 رو از 1.8 سیگما میرسونه به 3.5 سیگما که برای پک اون باید کلی هزینه و زحمت صرف بکنیم؛ و روش شماره 2 رو از 1.6 سیگما میرسونه به 2.3 سیگما که عملاً قابل پایش نیست.
چند تا نکته فرعی
گذشته از این که اساساً ایده تعدیل خطای مجاز اشتباهه و اصل موضوع اینه، اما روش به دست آوردن فرمول mTEa هم خالی از اشکال نیست و بد نیست نگاهی هم به اشکالات جنبی بندازیم.
اشکال اول اینه که نویسنده با بیان این که “اگر میزان مجاز هر یک از پارامترهای %Bias و %CV را معادل یک سوم %TEa در نظر بگیریم ” مقادیر مجاز جداگانه برای Bias و CV قائل میشه؛ در حالی که، همونطور که به طور کامل توضیح داده شد، همچین چیزی توی مدل خطای کل نداریم. اساساً مدل خطای کل ارائه شد که به جای صحبت از خطاهای مجاز جداگانه برای Bias و CV، خطای حاصل از این دو تا روی هم بذاریم بشه خطای سنجشی کل و مقدار مجاز برای این خطای کلی تعیین کنیم (TAE و TEa). واژه «کل» توی اسم این مدل به همین دلیله و به این موضوع اشاره داره. مثال صد هزار تومن اعتبار واسه خرید سیب و پرتقال رو یادمون بیاریم.
نمیشه بر اساس مدل خطای کل، به یه نفر گفت برو با این صد هزار تومن «خرید کل مجاز»، با هر ترکیبی که دوست داری سیب و پرتقال بخر و فقط حواست باشه «خرید کل» تو از صد هزار تومن بیشتر نشه و در عین حال به اون گفت «خرید مجاز سیب» اینقدره و «خرید مجاز پرتقال» اونقدر. نمیشه توی مدل خطای کل از خطاها مجاز جداگانه برای Bias و CV صحبت کرد. یا رومی روم یا زنگی زنگ؛ یا باید مثل بعضی کشورهای اروپاییها و همینطور مثل امریکای قبل از 1976، رویکرد خطاهای جداگانه برای Bias و CV رو انتخاب کرد، یا باید مثل امریکاییها و بعضی کشورهای دیگه، رویکرد خطای کل رو انتخاب کرد.
اشکال بعدی اینه که نویسنده، فرمول mTEa رو از فرمول %TAE = %Bias + 2%CV به دست میآره. نکته اینجاس که توی فرمول TAE، ضریب 2 یا دقیقتر بگیم 1.96 برای وقتییه که Bias برابر صفر باشه. در صورتی که Bias صفر باشه، 95% از سطح میانی زیر منحنی میافته تو فاصله X̄ ± 2%CV. اما در صورتی که Bias داشته باشیم، باید بسته به مقدار Bias، این ضریب رو کاهش بدیم. اگه فرمول کلی رو به صورت %TAE = %Bias + Z%CV بنویسیم، هر چی Bias از صفر برگتر بشه، باید Z از 1.96 کوچیکتر بشه. مثلاً وقتی که %Bias برابر CV میشه باید از Z برابر با 1.65 استفاده بکنیم. بعد از این که Bias از CV بزرگتر میشه، سرعت کاهش Z به ازای افزایش Bias خیلی کم میشه تا جایی که عملاً با 1.65 خیلی فرق نمیکنه.
به خاطر همینه که تو منابع جدید، با فرض وجود مقداری Bias (حداقل به اندازه CV)، از Z برابر با 1.65 توی فرمول خطای سنجشی کل استفاده میشه. و باز به همین دلیله که برای محاسبه «خطای کل مجاز بیولوژیک» از Z برابر با 1.65توی فرمول TE(%) = B(%) + 1.65*I(%) استفاده میشه تا وجود Bias در نظر گرفته شده باشه. از قضا، نویسنده فرض رو بر این میذاره که ” %Bias و %CV هردو معادل یک سوم %TEa” هستن. با این فرض، Bias با CV مساوییه و بنا بر این، دیگه ضریب 2 مناسب نیست و باید از ضریب 1.65 استفاده بشه. با این ضریب، فرمول متفاوتی واسه mTEa به دست میآد:
%TAE = %Bias + 1.65*%CV
%mTEa = %Bias + 1.65*(%CV/√n)
%mTEa = 1/3*%TEa + 1.65*[(1/3*%TEa)/√n] = 1/3*%TEa + (1.65*TEa)/(3*√n)
%mTEa = 2.65*%TEa/3√n
با این فرمول، اگه تکرار در کار نباشه و نمونهها فقط 1 بار سنجش بشن (n = 1):
%mTEa = 2.65*%TEa/3√1
%mTEa = ~0.88*%TEa!!!
با همچین فرمولی برای mTEa (که برای به دست آوردنش از مقدار درست برای Z استفاده شده) باید مدعی بشیم حتا بدون تکرار هم، باید خطای کل مجاز رو تعدیل کنیم (TEa رو در 0.88 ضرب بکنیم)!
نکته بعدی اینه که با شیوهای که نویسنده برای رسیدن به فرمول کلی mTEa استفاده میکنه، نمیشه برای تعدیل خطای کل بیولوژیک، TE(%)، فرمول کلی به دست آورد. این نکته از این نظر جالبه که TE(%) تنها خطای کلییه که از Bias مجاز و CV مجاز حساب میشه:
TE(%) = B(%) + 165I(%)
دلیل اینه که B(%) و I(%) هر کدوم معادل یک سوم TE(%) نیستن و بنا بر این B(%) و I(%) با هم برابر نیستن. هر آنالیت نسبتهای خاص خودش رو داره و B(%) و I(%) برای هر آنالیت، کسر خاصی از TE(%) رو تشکیل میده و بنا بر این، نمیشه به یه فرمول کلی mTEa برای مدل بیولوژیک رسید.
البته بازهم تأکید میکنم که اصل موضوع اینه که اساساً ایده تعدیل خطای مجاز اشتباهه؛ یعنی اساساً «چرایی» تعدیل خطای کل زیر سؤاله؛ و این سه نکته که گفتم اشکالاتی فرعییه توی «چگونگی» به دست آورن فرمول برای این تعدیل.
کلام آخر
با توضیحاتی که ارائه شده، بر اساس بدیهیات نباید خطای مجاز رو بسته به تلاشی که برای برآورده کردن اون میشه، تعدیل کرد. اول باید «چرایی» یه اقدام درست باشه، بعد بشینیم واسه «چگونگی» اون فرمول درست کنیم. اگه فقط ارائه فرمول کافی باشه، مثلاً اونهایی که ریاضی بلدن میتونن واسه سرگرمی با یه سری فرمول نشون بدن که 1 با 1 مساوی نیست. البته هم اون ریاضیبلدها و هم آدمهای ریاضینابلد مثل من، مساوی بودن 1 با 1 رو نمیپذیریم و میدونیم یه جایی توی اون فرمولها یه نکتهای هست که به چشم نمیاد.
علاوه بر این، اگه بنا باشه خطای کل مجاز رو تعدیل بکنیم، اون وقت دستاوردمون از تکرار سنجش نمونهها چی میشه؟ غیر از این که خطای مجاز، بیشتر و بیشتر آب بره تا جایی که از کوتاه شدن قد خطای ما جلو بزنه و عملکرد ما غیر قابل قبول بشه؟ غیر از این که احتمال پذیرفته نشدن نتایجمون بیشتر بشه؟ و غیر از این که عیار سیگمای روشمون تغییر چندانی نکنه، طوری که یا همچنان کیفیت روش ما قابل قبول نباشه یا این که اگه به سختی قابل قبول میشه، اینقدر جزئی باشه که قابل پایش نباشه (و عملاً قابل استفاده نباشه)؟ با این اوصاف، منطقییه بپرسیم چرا اصلاً باید اندازهگیریها رو به شکل تکراری انجام بدیم؟ چرا بیشتر زحمت بکشیم و بیشتر هزینه کنیم و دست آخر بدهکارتر بشیم؟ خوب از اول از خیر، ببخشید از شرّ، تکرار میگذریم.
نتیجه این که، mTEa ایده نادرستییه که از پیشفرضی نادرست مشتق شده و استفاده از اون برای ارزیابی تک-جوابها یا عملکرد، و همینطور هر کاربرد دیگهای شامل استفاده از mTEa توی بررسی خطی بودن، به نتیجهگیریهای اشتباه منجر میشه.
تشکر
از آقای محمد طالبی همکار علاقمند به مباحث پایش کیفیت، شاغل در آزمایشگاههای بیمارستان رازی و دکتر طیبی (قائمشهر) به خاطر ویرایش این نوشته سپاسگزارم. علاوه بر این، نامبرده با مطالعه جستجوگرانه و پرسشگرانه کتاب یاد شده و طرح نکاتی از کتاب با من، این انگیزه را در من به وجود آورد که این نقد را بنویسم.
[1] Callum G. Fraser; Per Hyltoft Petersen
همهی قوانین را نقض کنید – پاسخ به پرسشهای بخش نخست (n=1)
برای دانلود فایل pdf بر روی لینک زیر کلیک کنید
ورود / ثبت نام

بسم الله با سلام ، سوال بنده اینه که وقتی ما یک سیستم را مثلا اندازه گیری یک پارامتر را از لحاظ دقت وصحت یا درستی ویا میزان نزدیکی به مقدار درست اون اندازه میگیریم از وسایل وروشها وشرایطی باید استفاده کنیم حالا اگر بخواهیم ببینیم که کدام روش با کدام شرایط و با کدام دستگاه بهترین ودرسترین جواب را به ماخواهد داد برای جستن آن هیچ راهی بجز تکرار هم شرایط وهم متغیر برای اینکه نتایج قابل قیاس باهم باشند نداریم و از انجا که ما درکنترول کیفیت بدست آوردن مقدار درست را نه بلکه درواقع بدست اوردن اینکه چقدر خطا داریم مد نظر داریم پس درسته که بپرسیم وقتی ما فقط یکبار هرتست را انجام میدهیم درشرایط عادی باید توقع چه امکان یا احتمالی از بدست اوردن خطا را داشته باشیم که صد البته این یکبار با ان بیست بار هرگز یک رتبه را نخواهد داشت اما آن چندین بار تنها ارزشش اینه که به ما میگه چقدر خطا واقعا وجود داره که مکررا تکرار میشه ومسلما از یک حدی با وجود هرچقدر تکرار نمیتونه به صفر برسه ودر محدوده اندازه گیری های ما که قابل انجام هست تا حدی مشخص فقط میتونه کوچکتر وکوچکتر کنیم احتمال اینکه سنجش خطا یا یافتن مقدار خطاهامون را با آن دقت تا جای ممکن به حداقل تقلیل دهیم که بتواتیم بگوییم این روش نزدیک به حدود ۱۰۰ درصد یا ۹۹/۵درصد همین قدر خطا دارد حالا اگر ما بخواهیم این خطا را از این هم کمتر کنیم مث مثالی که زده اید دستگاهی از نوع اولی به تعداد دوتای دیگه اصافه گنیم که نه اتفاقی بلکه صد درصد راه حل مسیله اون انبار میوه هست چرا که این پارامتر برودت را میخواهیم با دستگاههای همسان در شرایط قبلی به کمتر تبدیل کنیم و این هیچ منافاتی با این مطلب ندارد که ما با دستگاههای دارای همان میزان خطای تولید برودت نتوانیم چنین کنیم و این فرض هم در اساس محال است. اما وقتی ما میخواهیم توانایی یک سیستم از انها را فقط از نظر مقدار خطایش بررسی کنیم مسلما با روشهای اندازه گیری وکنترول کیفیت فقط میتوانیم به پایش مقدار مجموع خطاهای موجود در عمل اون در شرایط رفته دست پیدا کنیم واینکه چند دستگاه را باهم بکار ببریم دیگه از همسانی شرایط درپایش خارج شده ایم ومسلمه که باید برای ان یک شرایط وخطای دیگر وسطح خطای دیگری مطرح کنیم چون درواقع ما فقط داریم مقدار خطا را درشرایط قبل یا فعلی میسنجیم واینکه بخواهیم با مقدار مجاز وآنچه که میخواهیم برسیم چگونه پس شرایط دیگری را خلق کنیم بله برای آن شرایط هم باید بتوانیم موارد دیگری از بهتر شدن مناسب ان خرج اصافه راهم لحاظ کنیم مثلا زودتر این برودت زیر ده درجه حاصل میشه واینکه بیشتر وپایدارتر باقی میمانه و اینکه در اتی به علت کمتر نیاز داشتن به صرف کار وبرق برای نگاهداری درجه دما مسلما راندمان بهتری هم خواهیم داشت شاید وجهه دیگر تعدیل شده هم همین است افزایش تعداد دستگاه ها اولا از سر مرز ایستادن در دمای ده درجه ما را رهانیده از اینکه ترموستات چقدر باید کار کنه وایا همیشه باید کارکنه مارا رهانیده واز اینکه این دودستگاه بعدی هرکدام چه مدت روشن خواهند شد وچه مدت خاموش میمانند تا دما در این درجه حفظ بماند مسلما به کاهش خطای پس محاسبه خطای تعدیل شده مجاز قابل قبول هم باید برسد .البته وصد البته ماهیت ونوع پارامتر اندازه گیری شده و… هم در نوع برخورد با هر مسئله یا مثالی دخیل هست البته نمیدونم که من کامل ودرست متوجه شدم مفاهیمی که شما پرسیدید واقای دکترطرح کرده اندرا یا خیر؟