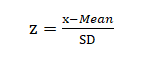همهی قوانین را نقض کنید! – پاسخهای بخش دوم
پاسخهای دومین بخش از سلسله مطالب مربوط به تفسیر اساسی پایش کیفیت. حالا میبینیم که اگر دو کنترل و نیاز به تفسیر بین مواد، بین سطوح، و بین دورها داشته باشیم، چه اتفاقی میافتد.
استن وستگارد، MS
نوامبر 2015
توضیح مترجم:
این سلسله مقالات شامل 6 بخش است که بهصورت ماهانه بر روی وبسایت Westgard.com قرار میگیرد. ترجمه و انتشار این مطالب در ماهنامهی اخبار آزمایشگاهی و نیز استفاده از طرح و بسایت یادشده با مجوز شرکت Westgard QC انجام میشود؛ امری که مایهی تقدیر و تشکر فراوان از متصدیان آن شرکت بهویژه جناب آقای استن وستگارد است.
ترجمهی بخش نخست در شمارهی 138 و ترجمهی پاسخ به پرسشهای بخش نخست و همچنین بخش دوم مقاله در شمارهی141 اخبار آزمایشگاهی تقدیم شد. اصل این مطالب و نیز اصل این بخش به ترتیب در نشانیهای زیر در وبسایت Westgard.com در دسترس است:
http://www.westgard.com/break-all-rules-1.htm
http://www.westgard.com/break-all-rules-answers1.htm
http://www.westgard.com/break-all-rules-2.htm
http://www.westgard.com/break-all-rules-answers2.htm
از آنجائی که ممکن است برخی مطالب مطرحشده در این مقالات نیازمند روشنگری بیشتری باشد، خوانندگان محترم میتوانند نکات، نظرات و پرسشهایشان را به رایانامهیlabnews2003@gmail.com ارسال کنند تا در شمارههای بعدی به بحث گذاشته شود.
قدردانی: بر خود لازم میدانم از جناب آقای دکتر محمدرضا عابدی سردبیر محترم این ماهنامه و همکاران تلاشگر ایشان به خاطر همکاری بیدریغ ایشان و از دوست و همکار گرامی جناب آقای دکتر مهدی صابونی به خاطر قبول زحمت ویرایش این مطالب صمیمانه تشکر نمایم.
حسن بیات؛ دانشآموختهی علوم آزمایشگاهی
همچنان به تلاشمان برای شکستن همهی “قوانین وستگارد” ادامه میدهیم. چنانکه بهزودی خواهیم دید، بخش نخست آسان بود – فقط مراقب یک کنترل بودیم. حال که دو کنترل در دست داریم، میخواهیم نگاه کردن از جهات گوناگون برای کشف خطاها را شروع کنیم.
دادهها – تبدیلشده به نمرهی z
به یاد بیاورید که میانگین کنترل پایین 47 و SD آن 3 است و میانگین کنترل بالا 71 و SD آن 8 است. بهجای کار کردن با ارقام “خام”، قصد داریم آنها را به نمرهی z تبدیل کنیم که نشان میدهد هر نقطه چند انحراف معیار از میانگین فاصله دارد[1]. به این طریق، پیدا کردن نقض قوانین آسانتر میشود.
| قانون نقض شده | نمرهی 2z | مقدار 2 | نمرهی 1z | مقدار 1 | اندازهگیری کنترل |
| 1.4 | 82.2 | 1.5 | 51.5 | 1 | |
| 2:2s با در نظر گرفتن هر دو کنترل | -2.5 | 51 | -2.7 | 38.9 | 2 |
| 0.4 | 74.2 | 0.2 | 47.6 | 3 | |
| 2.6 | 91.8 | -0.33 | 46.0 | 4 | |
| 0.4 | 74.2 | 1.3 | 50.9 | 5 | |
| -0.25 | 69.0 | 2.3 | 53.9 | 6 | |
| -1.6 | 58.2 | 1.9 | 52.7 | 7 | |
| 1:3s برای کنترل 2 | 3.06 | 95.5 | 0.7 | 49.1 | 8 |
| -0.7 | 65.4 | 0.5 | 48.5 | 9 | |
| 1:3s برای کنترل 1 و R:4s با هردو کنترل | 2.375 | 90.0 | -3.33 | 37.0 | 10 |
| -1 | 63.0 | 0 | 47.0 | 11 | |
| 1.4 | 82.2 | 2.33 | 54.0 | 12 | |
| 2:2s برای کنترل 1 | -0.7 | 65.4 | 2.1 | 53.3 | 13 |
| R:4s با محاسبه[2] | 1.9 | 86.2 | -2.33 | 40.0 | 14 |
| -0.1 | 70.2 | 2.8 | 55.4 | 15 | |
| 2.2 | 88.6 | 0.8 | 49.4 | 16 | |
| 2:2s برای کنترل 2 | 2.1 | 87.8 | -0.1 | 46.7 | 17 |
| 1.75 | 85.0 | -0.4 | 45.8 | 18 | |
| 0.7 | 76.6 | 1.9 | 52.7 | 19 | |
| -0.7 | 65.4 | 1.4 | 51.1 | 20 | |
| 1.9 | 86.2 | 2.33 | 54.0 | 21 | |
| 4:1s برای کنترل 1 و 2:2s برای کنترل 1 | 0 | 71.0 | 2 | 53.0 | 22 |
| 1.3 | 81.4 | 0.9 | 49.7 | 23 | |
| 2.4 | 90.2 | 0.4 | 48.2 | 24 | |
| 1.2 | 80.6 | -0.2 | 46.4 | 25 | |
| R:4s | -2.12 | 54.0 | 2.4 | 54.2 | 26 |
| -2.25 | 53 | 1.4 | 51.2 | 27 | |
| 0.7 | 76.6 | 2.3 | 53.9 | 28 | |
| 0.2 | 72.6 | -0.9 | 44.3 | 29 | |
| 1.7 | 84.6 | 0.5 | 48.5 | 30 |
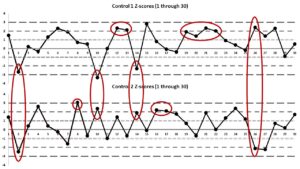
برای اینکه دیدن خطاها آسانتر شود، خطاهای مربوط به 30 نتیجهی نخست را روی نمودار لوی – جنینگز با درج نمرههای z مشخص کردهایم:
| قانون نقض شده | نمرهی 2z | مقدار 2 | نمرهی 1z | مقدار 1 | اندازهگیری کنترل |
| 1.8 | 85.4 | 0.5 | 48.5 | 31 | |
| 1.9 | 86.2 | 0.6 | 48.8 | 32 | |
| 1.12 | 80.0 | -0.1 | 46.7 | 33 | |
| 4:1s برای کنترل 2 | 1.11 | 79.9 | -0.3 | 46.1 | 34 |
| 1.6 | 83.8 | -0.33 | 46.0 | 35 | |
| -0.37 | 68.0 | 2.3 | 53.9 | 36 | |
| -0.8 | 64.6 | -1.33 | 43.0 | 37 | |
| 0 | 71.0 | -1.67 | 42.0 | 38 | |
| 1.5 | 83.0 | -2.33 | 40.0 | 39 | |
| 4:1s برای کنترل 1 | -0.5 | 67.0 | -1.5 | 42.5 | 40 |
| 0.4 | 74.2 | 1.1 | 50.3 | 41 | |
| 1:3s برای کنترل 2 | -3.12 | 46.0 | -0.9 | 44.3 | 42 |
| 0.1 | 71.8 | 1.6 | 51.8 | 43 | |
| -1.4 | 59.8 | -1.7 | 41.9 | 44 | |
| 4:1s با هر دو کنترل | -1.75 | 57.0 | -2.33 | 40.0 | 45 |
| -2 | 86.2 | 0.6 | 48.8 | 46 | |
| -0.12 | 55.0 | 2 | 53.0 | 47 | |
| 1 | 70.0 | 1.8 | 52.4 | 48 | |
| 1:3s برای کنترل 1 | -0.12 | 79.0 | -3 | 38.0 | 49 |
| -0.25 | 70.0 | 0.7 | 49.1 | 50 | |
| -0.25 | 69.0 | -1 | 44.0 | 51 | |
| 0.5 | 75.0 | 0.6 | 48.8 | 52 | |
| 0.7 | 76.6 | 1.2 | 50.6 | 53 | |
| 0.2 | 72.6 | -1.1 | 43.7 | 54 | |
| 1.12 | 80.0 | 0.2 | 47.6 | 55 | |
| 1 | 79.0 | -0.5 | 45.5 | 56 | |
| 0.37 | 74.0 | -0.9 | 44.3 | 57 | |
| 1.37 | 82.0 | 1.8 | 52.4 | 58 | |
| 8:x برای کنترل 2 | 0.12 | 72.0 | 2.3 | 53.9 | 59 |
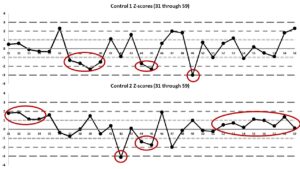
در اینجا مجموعهی دوم از نمودارهای لوی – جنینگز برای نتایج 31 تا 59 ارائه شده است:
| قانون نقض شده | نمرهی 2z | مقدار 2 | نمرهی 1z | مقدار 1 | اندازهگیری کنترل |
| 0.4 | 74.2 | -0.4 | 45.8 | 60 | |
| -0.8 | 64.6 | 1.2 | 50.6 | 61 | |
| 0 | 71.0 | 0.33 | 48.0 | 62 | |
| 1.5 | 83.0 | 0.67 | 49.0 | 63 | |
| -0.5 | 67.0 | 1.33 | 51.0 | 64 | |
| 0.4 | 74.2 | 2 | 53.0 | 65 | |
| 1.2 | 80.6 | 0.33 | 48.0 | 66 | |
| 0.1 | 71.8 | 0.67 | 49.0 | 67 | |
| 8:x برای کنترل 1 | -0.2 | 69.4 | 1 | 50.0 | 68 |
| 1.3 | 81.4 | 0.26 | 47.8 | 69 | |
| -0.7 | 65.4 | -0.5 | 45.5 | 70 | |
| -0.12 | 70.0 | -0.33 | 46.0 | 71 | |
| -0.25 | 69.0 | -0.67 | 45.0 | 72 | |
| 8:x با هر 2 کنترل | -0.62 | 66.0 | -0.33 | 46.0 | 73 |
| -0.3 | 68.6 | 0.3 | 47.9 | 74 | |
| 1.9 | 86.2 | 0.5 | 48.5 | 75 | |
| -1.4 | 59.8 | 1.3 | 50.9 | 76 | |
| -0.4 | 67.8 | -0.1 | 46.7 | 77 | |
| 1.9 | 86.2 | 0.26 | 47.8 | 78 | |
| 0.2 | 72.6 | 1.1 | 50.3 | 79 | |
| 1.3 | 81.4 | 1.67 | 52.0 | 80 | |
| 8:x با هر دو کنترل | 0.4 | 74.2 | 1.67 | 52.0 | 81 |
| 1.2 | 80.6 | 0.5 | 48.5 | 82 | |
| 1.1 | 79.8 | -0.9 | 44.3 | 83 | |
| 0.5 | 75.0 | 0.8 | 49.4 | 84 | |
| 0.7 | 76.6 | -0.1 | 46.7 | 85 | |
| 0.2 | 72.6 | 1.9 | 52.7 | 86 | |
| -1.9 | 55.8 | -0.6 | 45.2 | 87 | |
| 1 | 79.0 | 0.6 | 48.8 | 88 | |
| -0.1 | 70.2 | -0.2 | 46.4 | 89 | |
| 1.4 | 82.2 | 0.9 | 49.7 | 90 |
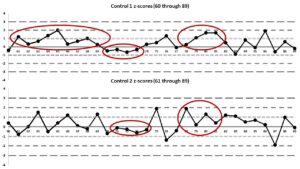
و بالاخره مجموعهی سوم نمودارهای لوی – جنینگز برای نتایج 60 تا 90:
شرطها را به یاد بیاورید:
- در هر دور دو کنترل میگذاریم؛ فرض کنید هر جفت از کنترلها نمایندهی یک دور است
- قصد نداریم نقض 2s را جستجو کنیم. بیایید از همین لحظه این عادت را ترک کنیم. به هر حال، من این دادهها را به صورت تصادفی تهیه نکردهام، بنابراین نباید انتظار داشته باشیم که شاهد تعداد معینی “رد کاذبهای طبیعی” به صورت دادههای پرت 2s باشیم.
- قصد نداریم دادههای پرت نسبت به “قوانین وستگارد” زیر را پیدا کنیم:
1:3s/2:2s/R:4s/4:1s/8:x
- قصد نداریم در باتلاق تکرار کنترلها فرو رویم. بنابراین گمان نکنید که هیچ یک از نتایجی را که میبینید حاصل تکرار کنترل است – فقط بر “درون” یا “بیرون” بودن مقادیر تمرکز کنید.
خوب، در پایان این بخش بررسی کنید آیا توانستید به پاسخهای زیر برسید؟
- موارد نقض قوانین چندتا بود؟ 17 مورد
- کدام قوانین نقض شده بودند و چند بار؟
- 1:3s (2 بار)
- 2:2s (4 بار)
- R:4s (3 بار)
- 4:1s (4 بار)
- نقض 8:x (4 بار)
- چه چیزی فرق میکرد اگر به شما میگفتم که فقط “قوانین وستگارد”1:3s/2:2s/R:4s لازم است؟
- در این صورت نقض 4:1s و 8:x نادیده گرفته میشد زیرا اینها دیگر خطاهای قابل ملاحظهای به شمار نمیآمدند.
- چه چیزی فرق میکرد اگر به شما میگفتم که فقط قانون پایش 1:3s لازم است؟
- فقط 3 یا 4 مورد نقض قانون دیده میشد.
- چه خطاهای کوچک دیگری که در این نمودارها و دادهها وجود دارد؟
[چیزی کم بود؟ آیا احساس میکنید جای چیزی خالی است؟ خواهش میکنم از این که توضیح بیشتری درخواست کنید، ابایی نداشته باشید.][3]
[1] مترجم: برای تبدیل یک نتیجه به نمرهی z، اختلاف آن نتیجه با میانگین را بر انحراف معیار تقسیم میکنیم:
[2] مترجم: معمولا نقض قانون R:4s به این شکل بیان میشود که یکی از نتایج پائینتر از 2s- باشد و دیگری بالاتر از 2s+ باشد؛ حال آن که بیان درستتر این است که بگوئیم هرگاه اختلاف جبری بین نتایج دو کنترل برابر یا بیش از 4s باشد این قانون نقض شده است.
در سال 1981 و هنگام انتشار اولین مقالهای که وستگارد و همکارانش در بارهی ترکیب قوانین نوشته بودند و در آن برای اولین بار مجموعه قوانینی را که بعدها به “قوانین وستگارد” مشهور شد معرفی کردند، یکی از داوران مجلهی کلینیکال کمسیتری (Robert W. Burnett) نظر داده بود که برای نقض قانون R4s لازم نیست حتما نتایج در دو سوی 2s- و 2s+ باشند، بلکه هرگاه اختلاف دو کنترل با محاسبهی جبری برابر یا بیش از 4 انحراف معیار شود این قانون نقض شده است (وی مثال زده بود که اگر مثلا نتیجهی یک کنترل برابر +2.5s و نتیجهی کنترل دیگر برابر 1.5s- باشد قانون R:4s نقض شده است زیرا اختلاف این دو نتیجه برابر 4s است). نویسندگان آن مقاله ضمن تایید نظر آن داور، علت روش پیشنهادی خود (یک نتیجه زیر 2s- و دیگری بالای 2s+) را اینطور مطرح کرده بودند که استفاده از قانون R4s به این شکل سادهتر است، در حالی که بررسی نقض آن به صورت محاسبهای بدون کامپیوتر سخت است. حال توجه داشته باشیم که در این روزگار که استفاده از برنامههای کامپیوتری امری بسیار معمول شده است، قانون R:4s باید به شکل درستتر آن یعنی به صورت محاسبهای بررسی شود.
یادآوری دیگر این است که قانون R:4s برای اختلاف کنترلها در یک دور استفاده میشود. به همین دلیل، نویسنده در مورد نقض این قانون فقط به ذکر R:4s بسنده کرده است و لازم ندیده است مشخص کند که این نقض با مقایسهی نتایج دو کنترل 1 و 2 با هم است؛ زیرا این قانون برای اختلاف یک کنترل با دور قبل اسفاده نمیشود. (بنا بر این برای استفاده از این قانون، باید بیش از یک کنترل در هر دور داشت).
مشخصات مقالهی یاد شده چنین است:
James 0. Westgard, Patricia L. Barry, Martin R. Hunt, Torgny Groth. CLIN. CHEM. 27/3, 493-501 (1981)
[3] جملات پایانی از متن اصلی است و توسط نویسنده درون قلاب گذاشته شده است. خوانندگانی که تمایل داشته باشند مطالبی را با نویسنده مطرح کنند میتوانند با نشانی westgard@westgard.com مکاتبه نمایند.
همهی قوانین را نقض کنید! (بخش دوم)
همهی قوانین را نقض کنید! (بخش نخست)
همهی قوانین را نقض کنید – پاسخ به پرسشهای بخش نخست (n=1)
برای دانلود پی دی اف بر روی لینک زیر کلیک کنید
ورود / ثبت نام